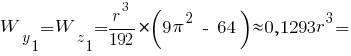Геометричні характеристики суцільних перерізів 017
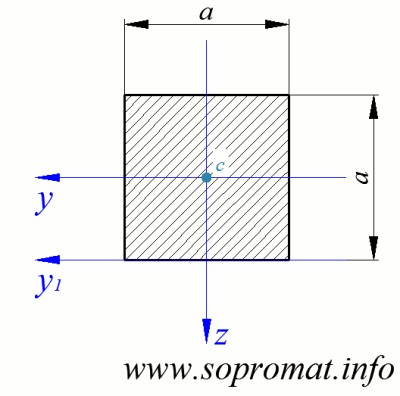

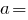
Площа квадрата:
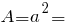
Головні моменти інерції квадрата:
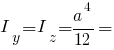
Інші осьові моменти інерції квадрата:
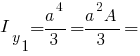
Полярний момент інерції квадрата:
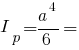
Головні радіуси інерції квадрата:
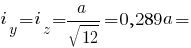
Головні моменти опору квадрата:
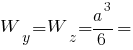
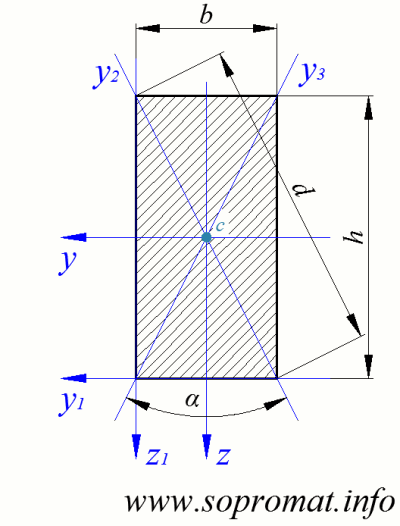

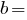
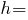
Площа прямокутника:
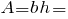
Головні моменти інерції прямокутника:
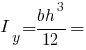
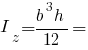
Інші моменти інерції прямокутника:
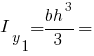
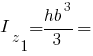
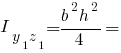
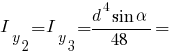
Полярний момент інерції прямокутника:
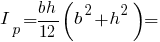
Головні радіуси інерції прямокутника:
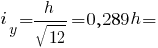
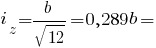
Головні моменти опору прямокутника:
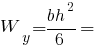
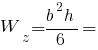

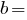
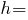 (
(
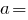 або
або
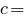 )
)
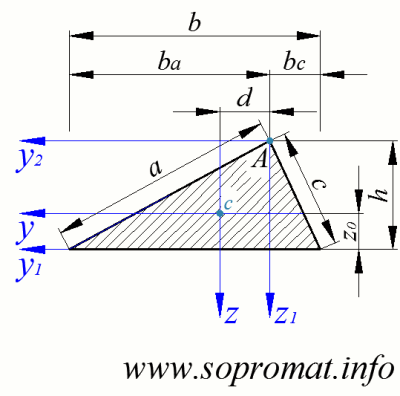
Площа трикутника:
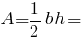
Центр ваги трикутника:
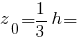
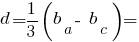
Розміри трикутника:
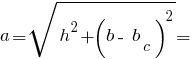
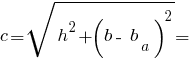
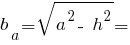
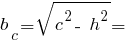
Моменти інерції трикутника:
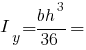
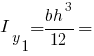
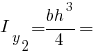
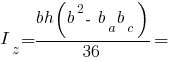
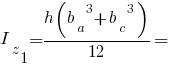
Полярні моменти інерції трикутника:
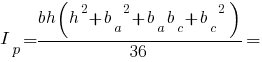
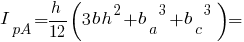
Радіуси інерції трикутника:
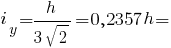
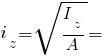
Моменти опору трикутника:
Верхні волокна:
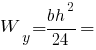
Нижні волокна:
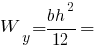
Ліві волокна:
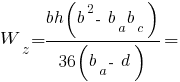
Праві волокна:
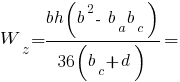
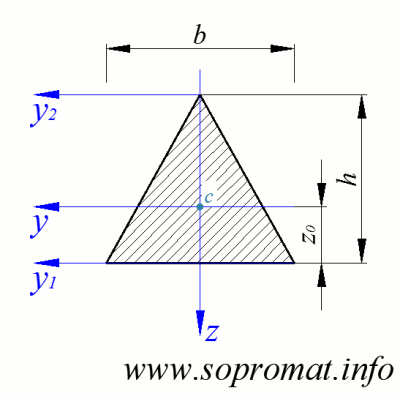

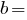
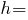
Площа рівнобедреного трикутника:
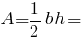
Центр ваги рівнобедреного трикутника:
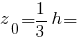
Головні моменти інерції рівнобедреного трикутника:
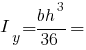
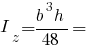
Інші моменти інерції рівнобедреного трикутника:
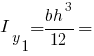
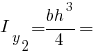
Полярний момент інерції рівнобедреного трикутника:
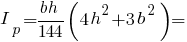
Головні радіуси інерції рівнобедреного трикутника:
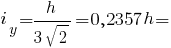
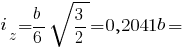
Головні моменти опору рівнобедреного трикутника:
Верхні волокна:
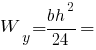
Нижні волокна:
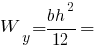
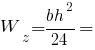
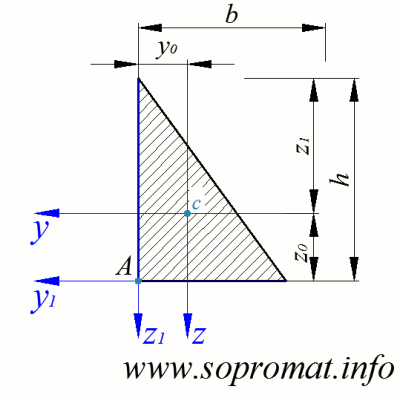

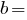
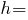
Площа прямокутного трикутника:
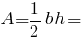
Центр ваги прямокутного трикутника:
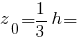
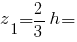
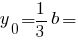
Моменти інерції прямокутного трикутника:
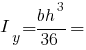
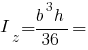
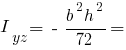
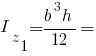
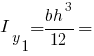
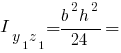
Полярні моменти інерції прямокутного трикутника:
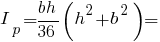
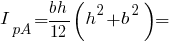
Радіуси інерції прямокутного трикутника:
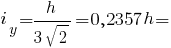
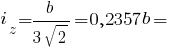
Моменти опору прямокутного трикутника:
Верхні волокна:
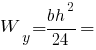
Нижні волокна:
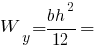
Ліві волокна:
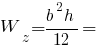
Праві волокна:
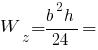
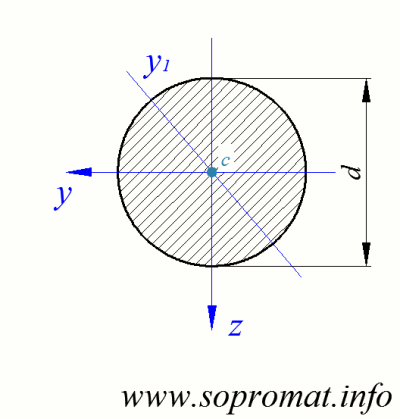

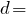
Площа кола:
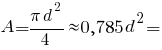
Головні моменти інерції кола:
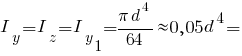
Полярний момент інерції кола:
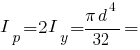
Головні радіуси інерції кола:
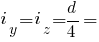
Головні моменти опору кола:
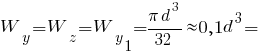
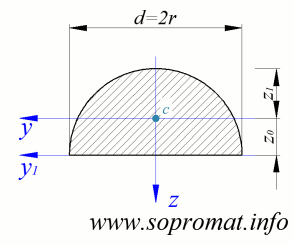

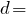
Площа півкола:
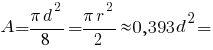
Центр ваги півкола:
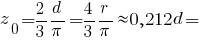
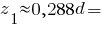
Головні моменти інерції півкола:
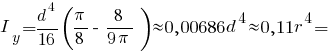
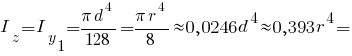
Головні радіуси інерції півкола:
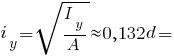
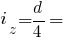
Головні моменти опору півкола:
Верхні волокна:
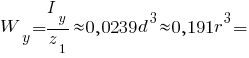
Нижні волокна:
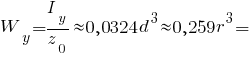
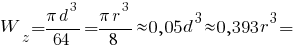
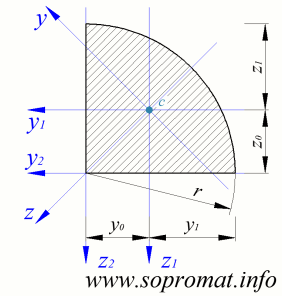

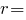
Площа чверть кола:
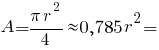
Центр ваги чверть кола:
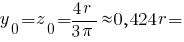
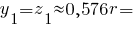
Головні моменти інерції чверть кола:
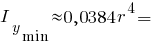
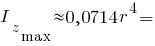
Інші моменти інерції чверть кола:
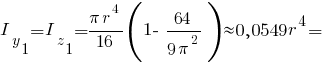
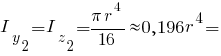
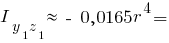
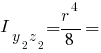
Головні радіуси інерції чверть кола:
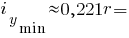
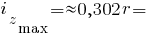
Моменти опору чверть кола:
Верхні та праві волокна:
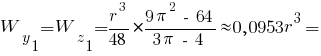
Нижні та ліві волокна: