Метод початкових параметрів (згин стержня) 016

Рис. 1

Кут повороту перерізу на відстані від початку координат:

;

Прогин на відстані від початку координат:

;

Початок координат знаходиться на лівому кінці стержня, вісь направлена вправо.

Тут - відстань від початку координат до перерізу, в якому визначаються кут повороту та прогин стержня.

- початкові параметри (прогин, кут повороту, згинальний момент та поперечна сила на початку стержня (з лівої сторони стержня).

- відповідно відстані від початку стержня до перерізів, в яких прикладені зосереджені момент 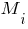, сила 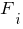, починається та закінчується дія рівномірно розподіленого навантаження 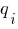(рис. 1).

- згинальна жорсткість стержня.

Переміщення, обчислені за наведеними формулами, одержуємо збільшеними в разів. Для визначення переміщень потрібно, щоб, крім зовнішніх навантажень, були відомі усі початкові параметри. Початкові зусилля беруться такими, що дорівнюють ординатам епюр та на лівому кінці балки. Початкові переміщення залежать від умов закріплення балки (рис. 2).

Рис. 2

Використовуючи формули переміщень, слід пам'ятати, що в них враховуються всі прикладені до балки зовнішні навантаження (враховуючи і реакції опор), які знаходяться з лівої сторони від розглядуваного перерізу.

Потрібно також звернути увагу на знаки величин, що входять у формули. Зовнішні навантаження, що мають напрями, вказані на рис. 1, підставляються із знаком "+", при протилежному напрямі будь-якого навантаження відповідні складові формули змінюють знак на протилежний. Правило знаків для переміщень таке: кут повороту за рухом годинникової стрілки, в прогин униз вважаються додатними.

Між функціями та інтенсивністю навантаження існують такі диференціальні залежності:

.

Потрібно стежити, щоб побудовані епюри відповідали наведеним залежностям (у розумінні правильного розташування точок екстремуму, перегину, нульових точок і т.п.).