Правило знаків для побудови епюр внутрішніх зусиль 019

внутрішні зусилля

Рис.1

Внутрішні зусилля в стержні (рис. 1):
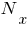N_x - поздовжнє зусилля,
Q_z - поперечне зусилля (паралельне осі ),
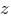M_y - згинальний момент відносно осі .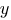

Зовнішнє навантаження, яке діє на стержень (рис. 1):
F_x - зосереджена поздовжня сила,
F_z - зосереджена поперечна сила,
- зосереджений згинальний момент,
- рівномірно розподілене навантаження.

Епюра поздовжніх сил

Рис. 2

Поздовжня сила в будь-якому перерізі стержня дорівнює сумі проекцій всіх сил (які знаходяться з одного боку від розглядуваного перерізу, зліва або справа) на поздовжню вісь стержня (рис. 2):

$N_x (x) = sum{i=1}{n}{F_{x~i}} + sum{i=1}{n}{q_{x~i} a_i}$ , або

$N_x (x) = sum{i=1}{n}{F_{x~i}} + sum{i=1}{n}{q_{x~i} delim{[}{(x ~-~ c_i) ~-~ (x ~-~ d_i)}{]}} = sum{i=1}{n}{F_{x~i}} + sum{i=1}{n}{q_{x~i} ( d_i ~-~ c_i )}$ .

правило знаків для епюри поздовжніх сил

Рис. 3

Правило знаків (рис. 3): додатня поздовжня сила направлена від перерізу (розтягує відсічену частину стержня), від'ємна - до перерізу (стискає відсічену частину стержня). При цьому розглядуваний переріз вважається нерухомим, а всі в'язі (опори) замінюються реакціями у в'язях.

Епюра поперечних сил

Рис. 4

Поперечна сила в будь-якому перерізі стержня дорівнює сумі проекцій всіх сил (які знаходяться з одного боку від розглядуваного перерізу, зліва або справа) на поперечну вісь стержня (рис. 4):

$Q_z (x) = sum{i=1}{n}{F_{z~i}} + sum{i=1}{n}{q_{z~i} a_i}$ , або

$Q_z (x) = sum{i=1}{n}{F_{z~i}} + sum{i=1}{n}{q_{z~i} delim{[}{(x ~-~ c_i) ~-~ (x ~-~ d_i)}{]}} = sum{i=1}{n}{F_{z~i}} + sum{i=1}{n}{q_{z~i} ( d_i ~-~ c_i )}$ .

правило знаків для епюри поперечних сил

Рис. 5

Правило знаків (рис. 5): додатня поперечна сила обертає відсічену частину стержня навколо розглядуваного перерізу за годинниковою стрілкою, від'ємна - проти. При цьому розглядуваний переріз вважається нерухомим, а всі в'язі (опори) замінюються реакціями у в'язях.

Епюра згинальних моментів

Рис. 6

Згинальний момент в будь-якому перерізі стержня дорівнює сумі моментів всіх сил (які знаходяться з одного боку від розглядуваного перерізу, зліва або справа) відносно розглядуваного перерізу (мається на увазі відносно однієї з поперечних осей перерізу) (рис. 6):

$M_y (x) = sum{i=1}{n}{M_{i}} + sum{i=1}{n}{F_{z~i} l_Fi} + sum{i=1}{n}{q_{z~i} a_i l_qi}$ , або

$M_y (x) = sum{i=1}{n}{M_{i}} + sum{i=1}{n}{F_{z~i} (x ~-~ b_i)} + sum{i=1}{n}{{q_{z~i}}/2 delim{[}{(x ~-~ c_i)^2 ~-~ (x ~-~ d_i)^2}{]}}$ .

правило знаків для епюри згинальних моментів

Рис. 7

Правило знаків (рис. 7): додатній згинальний момент розтягує нижні волокна, від'ємний - верхні. При цьому розглядуваний переріз вважається нерухомим, а всі в'язі (опори) замінюються реакціями у в'язях.

Момент - це добуток сили на плече. Плече - це найкоротша відстань (по перпендикуляру) від перерізу до лінії дії сили.

Епюра крутних моментів

Рис. 8

Крутний момент _кр в будь-якому перерізі стержня дорівнює сумі моментів всіх сил (які знаходяться з одного боку від розглядуваного перерізу, зліва або справа) відносно поздовжньої осі стержня (рис. 8):

$M_x (x) = sum{i=1}{n}{M_{kp~i}} + sum{i=1}{n}{m_{x~i} a_i}$ , або

$M_x (x) = sum{i=1}{n}{M_{kp~i}} + sum{i=1}{n}{m_{x~i} delim{[}{(x ~-~ c_i) ~-~ (x ~-~ d_i)}{]}} = sum{i=1}{n}{M_{kr~i}} + sum{i=1}{n}{m_{x~i} ( d_i ~-~ c_i )}$ .

правило знаків для епюри крутних моментів

Рис. 9

Правило знаків (рис. 9): додатній крутний момент обертає відсічену частину стержня навколо поздовжньої осі за годинниковою стрілкою, якщо дивитися зі сторони перерізу (тобто бачити торець відсіченої частини стержня), від'ємний - проти годинникової стрілки. При цьому розглядуваний переріз вважається нерухомим, а всі в'язі (опори) замінюються реакціями у в'язях.

Сподобалася стаття! Підтримай проект! Став ЛАЙК!

Для студента

Онлайн розрахунки

Реклама

Правило знаків для побудови епюр внутрішніх зусиль 019