Приклад 2. Розрахунок прокатної балки 044

|< < 1 2

Показано 2 по 2 із 2 (всього сторінок: 2)

4) Обчислюємо переміщення осі балки методом початкових параметрів.

Початкові параметри: w_0 = 0, ~~~ phi_0 = ?, ~~~ M_0 = 0, ~~~ Q_0 = ~-~ 15,64 кН.

Граничні та додаткові умови:

при x = 2 м right ~~w = 0 ;

при x = 6 м right ~~w = 0 .

Використовуючи формули для обчислення прогину осі балки методом початкових параметрів, запишемо:

$EI_y w(11) = EI_y phi_0 * 11 + 15,64 * {{11^3}/{6}} ~-~ 20 * {{(11 ~-~ 4)^3}/{6}} + 18 * {{(11 ~-~ 9)^2}/{2}} = 0$ ;

або

EI_y phi_0 * 11 = 2362,14 .

Розв’язуючи, знаходимо:

EI_y phi_0 = ~-~ 214,67 кН·м ² рад.

Ділимо балку на ділянки та визначаємо значення кута повороту і прогину в характерних точках (на границях ділянок та посередині кожної ділянки,
рис. 2).

Складаємо вирази для кута повороту і прогину для кожної ділянки та обчислюємо значення EI_y phi і EI_y w .

Перша ділянка ( 0<=x<=4 м)

$EI_y phi(x) = ~-~ 214,67 + 15,64 * {{x^2}/{2}}$ ;

$EI_y w(x) = ~-~ 214,67 * x + 15,64 * {{x^3}/{6}}$ .

x = 0

EI_y phi(0) = ~-~ 214,67 кН·м ² рад;

EI_y w(0) = 0 кН·м ³.

x = 2 м

$EI_y phi(2) = ~-~ 214,67 + 15,64 * {{2^2}/{2}} = ~-~ 183,39$ кН·м ² рад;

$EI_y w(2) = ~-~ 214,67 * 2 + 15,64 * {{2^3}/{6}} = ~-~ 408,48$ кН·м ³.

x = 4 м

$EI_y phi(4) = ~-~ 214,67 + 15,64 * {{4^2}/{2}} = ~-~ 89,58$ кН·м ² рад;

$EI_y w(4) = ~-~ 214,67 * 4 + 15,64 * {{4^3}/{6}} = ~-~ 691,88$ кН·м ³.

Друга ділянка ( 4<x<=9 м)

$EI_y phi(x) = ~-~ 214,67 + 15,64 * {{x^2}/{2}} ~-~ 20 * {{(x ~-~ 4)^2}/{2}}$ ;

$EI_y w(x) = ~-~ 214,67 * x + 15,64 * {{x^3}/{6}} ~-~ 20 * {{(x ~-~ 4)^3}/{6}}$ .

x = 6,5 м

$EI_y phi(6,5) = ~-~ 214,67 + 15,64 * {{6,5^2}/{2}} ~-~ 20 * {{(6,5 ~-~ 4)^2}/{2}} = 53,15$ кН·м ² рад;

$EI_y w(6,5) = ~-~ 214,67 * 6,5 + 15,64 * {{{6,5}^3}/{6}} ~-~ 20 * {{(6,5 ~-~ 4)^3}/{6}} = ~-~ 731,73$ кН·м ³.

x = 9 м

$EI_y phi(9) = ~-~ 214,67 + 15,64 * {{9^2}/{2}} ~-~ 20 * {{(9 ~-~ 4)^2}/{2}} = 168,61$ кН·м ² рад;

$EI_y w(9) = ~-~ 214,67 * 9 + 15,64 * {{9^3}/{6}} ~-~ 20 * {{(9 ~-~ 4)^3}/{6}} = ~-~ 448,85$ кН·м ³.

Третя ділянка ( 9<x<=11 м)

$EI_y phi(x) = ~-~ 214,67 + 15,64 * {{x^2}/{2}} ~-~ 20 * {{(x ~-~ 4)^2}/{2}} + 18 * (x ~-~ 9)$ ;

$EI_y w(x) = ~-~ 214,67 * x + 15,64 * {{x^3}/{6}} ~-~ 20 * {{(x ~-~ 4)^3}/{6}} + 18 * {{(x ~-~ 9)^2}/{2}}$ .

x = 10 м

$EI_y phi(10) = ~-~ 214,67 + 15,64 * {{10^2}/{2}} ~-~ 20 * {{(10 ~-~ 4)^2}/{2}} + 18 * (10 ~-~ 9) = 225,15$ кН·м ² рад;

$EI_y w(10) = ~-~ 214,67 * 10 + 15,64 * {{10^3}/{6}} ~-~ 20 * {{(10 ~-~ 4)^3}/{6}} + 18 * {{(10 ~-~ 9)^2}/{2}} = ~-~ 251,61$ кН·м ³.

x = 11 м

$EI_y phi(11) = ~-~ 214,67 + 15,64 * {{11^2}/{2}} ~-~ 20 * {{(11 ~-~ 4)^2}/{2}} + 18 * (11 ~-~ 9) = 277,33$ кН·м ² рад;

$EI_y w(11) = ~-~ 214,67 * 11 + 15,64 * {{11^3}/{6}} ~-~ 20 * {{(11 ~-~ 4)^3}/{6}} + 18 * {{(11 ~-~ 9)^2}/{2}} = 0$ кН·м ³.

Четверта ділянка ( 11<x<=16 м)

$EI_y phi(x) = ~-~ 214,67 + 15,64 * {{x^2}/{2}} ~-~ 20 * {{(x ~-~ 4)^2}/{2}} + 18 * (x ~-~ 9) ~-~ 15,64 * {{(x ~-~ 11)^2}/{2}} + 4 * {{(x ~-~ 11)^3}/{6}}$ ;

$EI_y w(x) = ~-~ 214,67 * x + 15,64 * {{x^3}/{6}} ~-~ 20 * {{(x ~-~ 4)^3}/{6}} + 18 * {{(x ~-~ 9)^2}/{2}} ~-~ 15,64 * {{(x ~-~ 11)^3}/{6}} + 4 * {{(x ~-~ 11)^4}/{24}}$ .

x = 13,5 м

$EI_y phi(13,5) = ~-~ 214,67 + 15,64 * {{13,5^2}/{2}} ~-~ 20 * {{(13,5 ~-~ 4)^2}/{2}} + 18 * (13,5 ~-~ 9) ~-~$
$~-~ 15,64 * {{(13,5 ~-~ 11)^2}/{2}} + 4 * {{(13,5 ~-~ 11)^3}/{6}} = ~-~ 350,25$ кН·м ² рад;

$EI_y w(13,5) = ~-~ 214,67 * 13,5 + 15,64 * {{13,5^3}/{6}} ~-~ 20 * {{(13,5 ~-~ 4)^3}/{6}} + 18 * {{(13,5 ~-~ 9)^2}/{2}} ~-~$
$~-~ 15,64 * {{(13,5 ~-~ 11)^3}/{6}} + 4 * {{(13,5 ~-~ 11)^4}/{24}} = 804,01$ кН·м ³.

x = 16 м

$EI_y phi(16) = ~-~ 214,67 + 15,64 * {{16^2}/{2}} ~-~ 20 * {{(16 ~-~ 4)^2}/{2}} + 18 * (16 ~-~ 9) ~-~$
$~-~ 15,64 * {{(16 ~-~ 11)^2}/{2}} + 4 * {{(16 ~-~ 11)^3}/{6}} = ~-~ 360,67$ кН·м ² рад;

$EI_y w(16) = ~-~ 214,67 * 16 + 15,64 * {{16^3}/{6}} ~-~ 20 * {{(16 ~-~ 4)^3}/{6}} + 18 * {{(16 ~-~ 9)^2}/{2}} ~-~$
$~-~ 15,64 * {{(16 ~-~ 11)^3}/{6}} + 4 * {{(16 ~-~ 11)^4}/{24}} = 1699,17$ кН·м ³.

За визначеними ординатами будуємо епюри EI_y phi та EI_y w (рис. 2).

5) Графоаналітичний метод.

Графоаналітичним методом визначаємо кут повороту та прогин перерізу при x = 4 м. Креслимо фіктивну балку (рис. 4), завантажуємо її розподіленим фіктивним навантаженням (епюрою згинальних моментів), яке замінюється фіктивними рівнодіючими:

${P_1}$ ^ф ~ = {1/2} * 4 * 62,55 = 125,1 кН·м ²; ${P_2}$ ^ф ~ = {1/2} * 5 * (62,55 ~-~ 40,73) = 54,55 кН·м ²;

${P_3}$ ^ф ~ = 5 * 40,73 = 203,65 кН·м ²; ${P_4}$ ^ф ~ = {1/2} * 2 * (58,73 ~-~ 50) = 8,73 кН·м ²;

${P_5}$ ^ф ~ = 2 * 50 = 100 кН·м ²; ${P_6}$ ^ф $~ = {ql^3}/{6} = {4 * 5^3}/{6} = 83,33$ кН·м ².

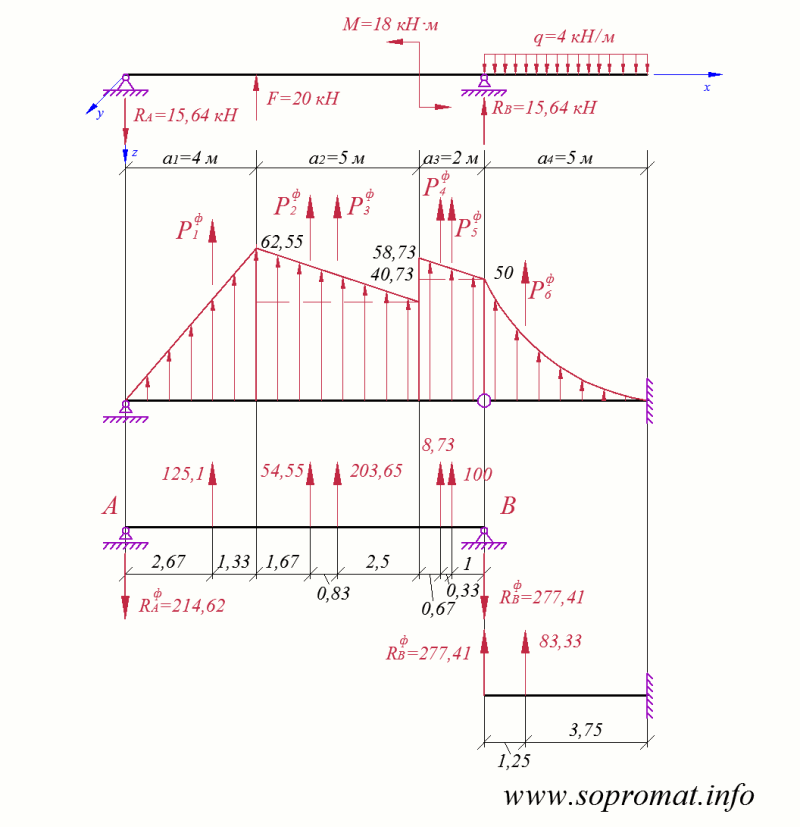
графо-аналітичний метод визначення переміщень при згині

Рис. 4

Обчислюємо фіктивні опорні реакції:

$sum{~}{~}{M_A} = 0,~~ R_B$ ^ф *11 ~-~ 125,1*2,67 ~-~ 54,55*5,67 ~-~ 203,65*6,5 ~-~ 8,73*9,67 ~-~ 100*10 = 0,
~~ R_B ^ф ~= 277,41 кН·м ²;

$sum{~}{~}{M_B} = 0,~~ ~-~ R_A$ ^ф *11 + 125,1*8,33 + 54,55*5,33 + 203,65*4,5 + 8,73*1,33 + 100*1 = 0,
~~ R_A ^ф ~= 214,62 кН·м ².

Виконуємо перевірку: $sum{~}{~}{F_z} = 0,~~ 214,62 ~-~ 125,1 ~-~ 54,55 ~-~ 203,65 ~-~ 8,73 ~-~ 100 + 277,41= 0$ .

Визначаємо значення EI_y phi та EI_y w при x = 4 м:

EI_y phi = ~-~ 214,62 + 125,1 = ~-~ 89,52 кН·м ² рад;

EI_y w = ~-~ 214,62 * 4 + 125,1 * 1,33 = ~-~ 692,1 кН·м ³.

6) Метод Мора.

Для визначення кута повороту та прогину в перерізі при x = 4 м методом Мора розглядаємо три стани балки: вантажний та два одиничних (рис. 5).

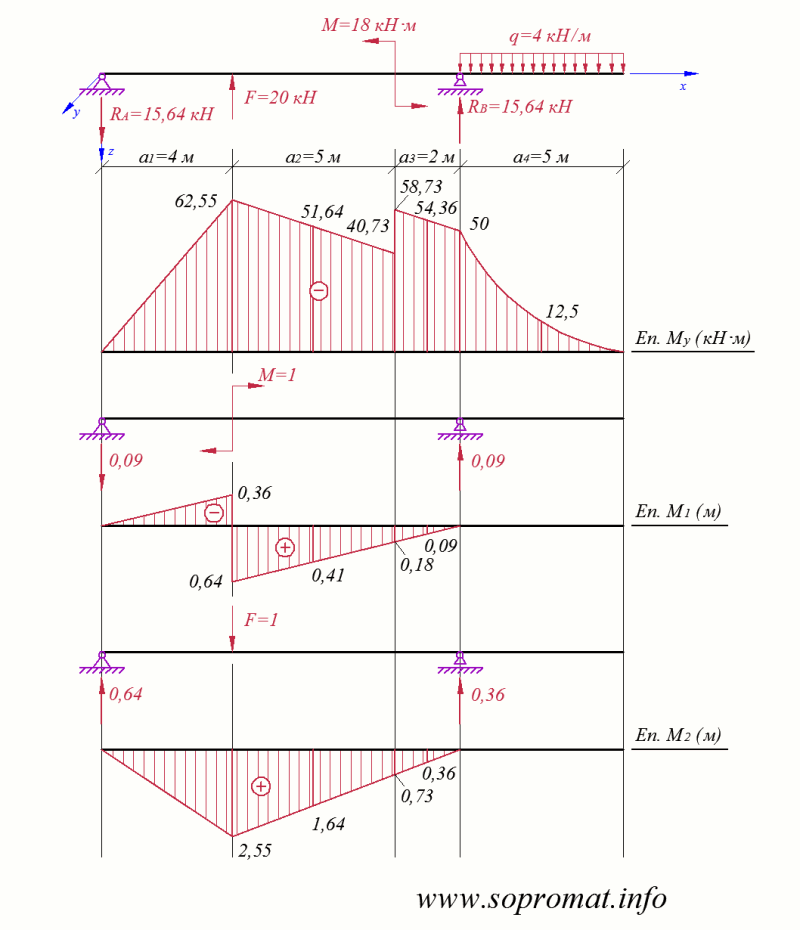
метод мора визначення переміщень при згині

Рис. 5

Перемножуючи епюри M_1 та M_2 на епюру M_y (з використанням правила Верещагіна та формули Сімпсона-Корноухова) отримуємо:

$EI_y phi = int{0}{l}{M_1 M_y dx} = {1/2} * 4 * 62,55 * {2/3} * 0,36 + {5/6} * (~-~ 62,55 * 0,64 ~-~ 4 * 51,64 * 0,41 ~-~ 40,73 * 0,18) +$ + {2/6} * (~-~ 58,73 * 0,18 ~-~ 4 * 54,36 * 0,09)= ~-~ 90,07 кН·м ² рад;

$EI_y w = int{0}{l}{M_2 M_y dx} = ~-~{1/2} * 4 * 62,55 * {2/3} * 2,55 + {5/6} * (~-~ 62,55 * 2,55 ~-~ 4 * 51,64 * 1,64 ~-~ 40,73 * 0,73) +$ + {2/6} * (~-~ 58,73 * 0,73 ~-~ 4 * 54,36 * 0,36)= ~-~ 693,05 кН·м ³.