Приклад 3. Побудова епюр зусиль у шарнірній балці 032

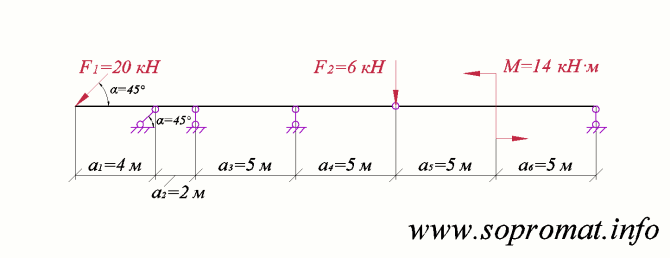
Рис. 1

Дано розрахункову схему шарнірної балки (рис. 1) та прикладене до неї зовнішнє навантаження.

Потрібно:
1) Визначити опорні реакції.
2) Побудувати епюри внутрішніх зусиль: епюру поздовжніх сил (рис. 2, Еп.N_x), поперечних сил (рис. 2, Еп.Q_z) та згинальних моментів (рис. 2, Еп.M_y).

Розв'язок:

1) Визначення опорних реакцій.

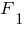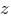Спроектуємо силу на осі та (рис. 2).
Її проекції рівні:
кН;
кН.

Оскільки в наскрізному шарнірі згинальний момент дорівнює нулю, то балку, зображену на рис.1, можна розраховувати як дві окремі балки (рис. 2, I, II). Розрахунок починаємо з балки, в якій кількість опорних реакцій відповідає кількості рівнянь статичної рівноваги статики (для плоских задач - три рівняння). Опорна реакція (де знаходиться шарнір) першої балки, передається на інші балки з протилежним знаком.

I - балка

Сума моментів всіх сил відносно точки :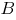
;
;
кН.

Сума моментів всіх сил відносно точки :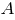
;
;
кН.

II - балка

Сума проекцій всіх сил на вісь :
;
;
кН.

Сума моментів всіх сил відносно точки :
Оскільки трикутник - прямокутний рівнобедрений трикутник, то м.
;
;
кН.

Сума моментів всіх сил відносно точки :
Оскільки трикутник - прямокутний рівнобедрений трикутник, то м.
;
;
кН.

Перевірка (сума проекцій всіх сил на вісь ):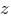
.

2) Побудова епюр внутрішніх зусиль.

Позначаємо характерні точки та визначаємо в них значення зусиль, використовуючи відповідне правило знаків для побудови епюр внутрішніх зусиль.

Побудова епюри поздовжніх сил (Еп.N_x, кН):
^Л;
^Пр.

Будуємо епюру поздовжніх сил (рис.2).

Побудова епюри поперечних сил (Еп.Q_z, кН):
^Л;
^Пр;
^Л;
^Пр;
^Л;
^Пр;
^Л;
^Пр;
^Л;
^Пр.

Будуємо епюру поперечних сил (рис.2).

Побудова епюри згинальних моментів (Еп.M_y, кН·м):
;
^Пр;
^Л;
;
;
;
;
.

Будуємо епюру згинальних моментів (рис.2).

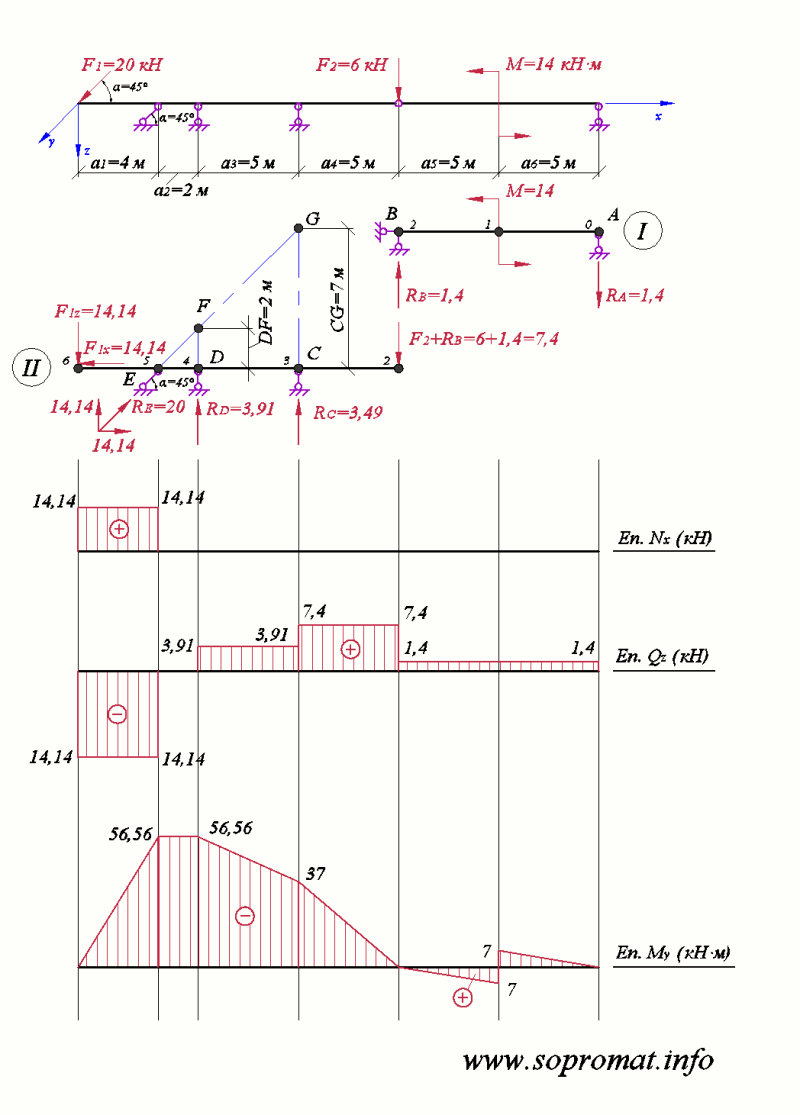
Рис. 2