Приклад 5. Побудова епюр зусиль у двохопорній балці 035

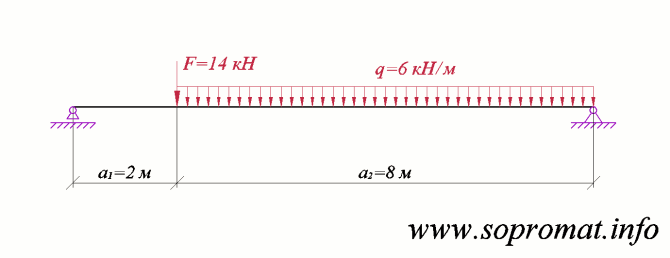
Рис. 1

Дано розрахункову схему двохопорної балки (рис. 1) та прикладене до неї зовнішнє навантаження.

Потрібно:
1) Визначити опорні реакції.
2) Побудувати епюри внутрішніх зусиль: епюру поперечних сил (рис. 2, Еп.Q_z) та згинальних моментів (рис. 2, Еп.M_y).

Розв'язок:

1) Визначення опорних реакцій.

Сума моментів всіх сил відносно точки :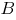
;
;
кН.

Сума моментів всіх сил відносно точки :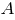
;
;
кН.

Перевірка (сума проекцій всіх сил на вісь ):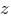
.

2) Побудова епюр внутрішніх зусиль.

Позначаємо характерні точки та визначаємо в них значення зусиль, використовуючи відповідне правило знаків для побудови епюр внутрішніх зусиль.

Побудова епюри поперечних сил (Еп.Q_z, кН):
^Пр;
^Л;
^Пр;
^Л.

На епюрі Еп.Q_z визначаємо координату точки де :

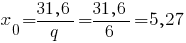м.

Будуємо епюру поперечних сил (рис.2).

Побудова епюри згинальних моментів (Еп.M_y, кН·м):
;
;
;
.

Визначаємо екстремум на епюрі згинальних моментів:

м.

Будуємо епюру згинальних моментів (рис.2).

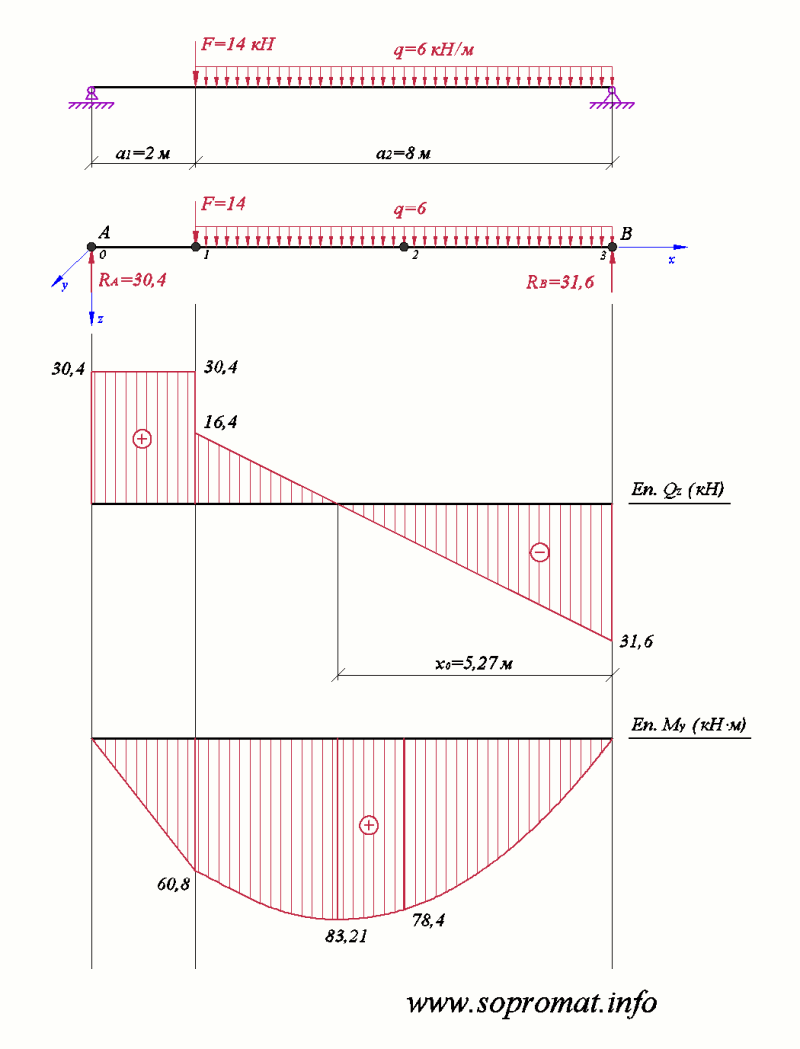
Рис. 2