Геометричні характеристики плоского поперечного перерізу 3 елементи (смуга, двотавр, кутник) 018

Рис. 1 |
Дано схему поперечного перерізу, складену з трьох елементів (рис. 1). Визначити геометричні характеристики складеного поперечного перерізу. Площу, центр ваги, положення головних осей, головні моменти інерції, головні радіуси інерції, головні моменти опору та побудувати еліпс інерції.
План виконання задачі: |
1) Виписуємо з таблиці сортаменту (ГОСТ 8239-72 та ГОСТ 8509-86) необхідні геометричні характеристики для двотавра, кутника та обчислюємо за формулами прямокутника:
а) Смуга (прямокутник) 200Х16
 |
 см 2, см 2, см 4, см 4, см 4, см 4, |
б) Двотавр №16
 |
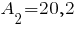 см 2, см 2,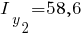 см 4, см 4,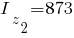 см 4, см 4,  см, см, см. см. |
в) Кутник 90Х6
 |
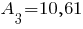 см 2, см 2,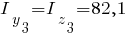 см 4, см 4, см 4, см 4,  см 4, см 4, см, см, см. см. |
2) Визначаємо положення центру ваги перерізу відносно початкових осей (осей смуги) 
На окремому аркуші паперу в масштабі креслимо схему поперечного перерізу (рис. 2) та вказуємо положення центральних осей кожного елементу. Виконуємо прив'язку (вказуємо відстані) центрів ваги кожного елементу відносно початкових осей 
Координати центрів ваги елементів в осях 

 см,
см,
 см,
см,

 см,
см,
 см.
см.

Рис. 2
Площа поперечного перерізу:
 см 2,
см 2,
Координати центру ваги перерізу:
 см,
см,
 см.
см.
Відкладаємо на рисунку координати  та
та  з урахуванням знаків, позначаємо положення центру ваги (точка С) та проводимо центральні осі
з урахуванням знаків, позначаємо положення центру ваги (точка С) та проводимо центральні осі 
Контролюємо достовірність визначення положення центру ваги складного перерізу. Для цього обчислюємо координати центрів ваги елементів перерізу в координатних осях  та
та  (відстані між власними центральними осями окремих елементів і центральними осями перерізу):
(відстані між власними центральними осями окремих елементів і центральними осями перерізу):
|
|
|
та статичні моменти площі перерізу відносно центральних осей:
 см 3,
см 3,
похибка: 
 см 3,
см 3,
похибка: 
3) На основі формул паралельного переходу обчислюємо моменти інерції перерізу відносно центральних осей  та
та 
- осьові

 см 4,
см 4,

 см 4,
см 4,
- відцентровий

 см 4.
см 4.
4) Визначаємо положення головних центральних осей інерції:

Звідси 
На рисунку відкладаємо додатній кут проти годинникової стрілки й креслимо головні центральні осі інерції (рис. 3).
5) Для визначення величин головних центральних моментів інерції використовуємо три види формул.
а)

 см 4,
см 4,

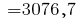 см 4,
см 4,
Для перевірки правильності знаходження головних моментів інерції, визначаємо відцентровий момент інерції відносно головних осей:

 ,
,
похибка: 
б)
 см 4,
см 4,
 см 4,
см 4,
в)

 .
.
Оскільки  , то
, то 
 см 4,
см 4,
 см 4.
см 4.
Перевіряємо умову інваріантності осьових моментів інерції:

 см 4,
см 4,
 см 4.
см 4.
6) Обчислюємо головні радіуси інерції:
 см,
см,
 см,
см,
та будуємо еліпс інерції (рис. 3). Визначаємо графічно радіуси інерції відносно осей 
 см,
см, см.
см.
Обчислюємо моменти інерції відносно цих осей:
 см 4,
см 4,
 см 4,
см 4,
та порівнюємо з раніше обчисленими значеннями:
 см 4,
см 4, см 4.
см 4.
7) Визначаємо головні моменти опору  та
та 
Найбільш віддаленою точкою від осі  є точка
є точка  а від осі
а від осі  - точка
- точка  Вимірюючи на рисунку відстані до цих точок від відповідних головних осей, знаходимо:
Вимірюючи на рисунку відстані до цих точок від відповідних головних осей, знаходимо: 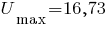 см,
см, 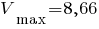 см.
см.
Перевіряємо за формулами:
 см,
см,
 см.
см.
Головні моменти опору:
 см 3,
см 3,
 см 3.
см 3.

Рис. 3



 см,
см, см,
см, см.
см.
 см,
см, см,
см, см.
см.