Приклад 1. Визначення моментів інерції відносно заданих осей (2 прокатних елемента) 021

геометричні характеристики складеного поперечного перерізу

Рис. 1

Дано схему поперечного перерізу, складену з двох елементів (рис. 1). Визначити осьові моменти інерції та відцентровий момент інерції відносно заданих осей.

План виконання задачі:
1) Геометричні характеристики елементів перерізу.
2) Визначення моментів інерції відносно допоміжних осей.
3) Визначення моментів інерції відносно заданих осей.

1) Виписуємо з таблиці сортаменту (ГОСТ 8240-72 та ГОСТ 8509-86) необхідні геометричні характеристики для швелера та кутника:

а) Швелер №16

см ²,

см ⁴,

см ⁴,
$I_{{y_1}{z_1}}=0 ,$
b=6,4

см,

см.

б) Кутник 70Х10

см ²,

см ⁴,

см ⁴,
$I_{{y_2}{z_2}}= pm(I_max ~-~ I_y_3 )=$
= ~-~(91,52 ~-~ 57,9) = ~-~33,62

см ⁴,

см,

см.

2) Визначаємо моменти інерції відносно допоміжних осей .

На окремому аркуші паперу в масштабі креслимо схему поперечного перерізу (рис. 2) та вказуємо положення центральних осей кожного елементу. Паралельно центральним осям елементів перерізу через точку нуль проводимо допоміжні осі y_0 ,~z_0 . Виконуємо прив'язку (вказуємо відстані) центрів ваги кожного елементу відносно допоміжних осей .

Координати центрів ваги елементів в осях y_0 ,~z_0 :

y_01 = 16/2 = 8 см,

y_02 = 16 ~-~ 2,1 = 13,9 см,

z_01 = ~-~1,8 см,

z_02 = 7 ~-~ 2,1 = 4,9 см.

складений переріз

Рис. 2

На основі формул паралельного переходу обчислюємо моменти інерції перерізу відносно допоміжних осей y_0 та z_0 :

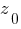- осьові моменти інерції

$I_y_0=sum{i=1}{2}{(I_y_i+{z_{0i}}^2 A_i)}= 63,3 + {(~-~1,8)}^2*18,1 + 57,9 + {4,9}^2*13,11 = 494,62$ см ⁴,

$I_z_0=sum{i=1}{2}{(I_z_i+{y_{0i}}^2 A_i)}= 747 + {8}^2*18,1 + 57,9 + {13,9}^2*13,11 = 4496,28$ см ⁴,

- відцентровий момент інерції

$I_{{y_0}{z_0}}=sum{i=1}{2}{(I_{{y_i}{z_i}}+{y_{0i}} {z_{0i}} A_i)} = 0 + 8*(~-~1,8)*18,1 + (~-~33,62) + 13,9*4,9*13,11 = 598,66$ см ⁴.

3) Визначаємо моменти інерції відносно заданих осей .

моменти інерції при повороті осей

Рис. 3

На рис. 3 під заданим кутом проводимо осі y_p ,~z_p . Визначаємо найменший кут alpha ~(beta) , на який потрібно повернути допоміжні осі y_0 ,~z_0 , так щоб вони співпали з осями .

alpha = 180^circ ~-~ 20^circ = 160^circ , ~(beta = ~-~20^circ) .

Для визначення моментів інерції відносно заданих осей, використовуємо формули визначення моментів інерції при повороті координатних осей:

- осьові моменти інерції відносно шуканих осей

$I_y_p={I_y_0}cos^2{alpha}+{I_z_0}sin^2{alpha}~-~{I_{{y_0}{z_0}}}sin{2{alpha}}= 494,62 cos^2{160^circ} + 4496,28 sin^2{160^circ} ~-~$
$~-~ 598,66 sin{2*160^circ} = 1347,53$ см ⁴,

$I_z_p={I_y_0}sin^2{alpha}+{I_z_0}cos^2{alpha}+{I_{{y_0}{z_0}}}sin{2{alpha}}= 494,62 sin^2{160^circ} + 4496,28 cos^2{160^circ} +$
$+ 598,66 sin{2*160^circ} = 3643,36$ см ⁴,

- відцентровий момент інерції відносно шуканих осей

$I_{y_p z_p} = I_{{y_0}{z_0}} cos{2alpha} + 1/2 ( I_y_0 ~-~ I_z_0 ) sin{2alpha} = 598,66 cos{2*160^circ} +$
$+ 1/2 (494,62 ~-~ 4496,28) sin{2*160^circ} = 1744,71$ .

Сподобалася стаття! Підтримай проект! Став ЛАЙК!

Для студента

Онлайн розрахунки

Реклама

Приклад 1. Визначення моментів інерції відносно заданих осей (2 прокатних елемента) 021