Приклад 1. Розрахунок прокатної балки 022
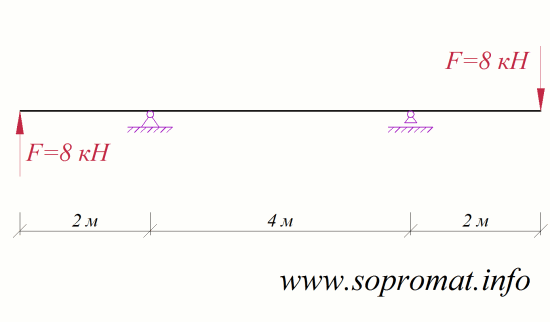
Рис. 1
|
Дано: схема балки з навантаженням (рис. 1), допустимі напруження Потрібно: визначити опорні реакції, побудувати епюри внутрішніх зусиль, підібрати переріз балки з двотавра та перевірити міцність прийнятого перерізу, побудувати епюри переміщень, методом Мора і графоаналітичним методом в довільному перерізі балки визначити кут повороту та прогин. |
План виконання задачі: 1) Визначення опорних реакцій та побудова епюр внутрішніх зусиль. 2) Підбір поперечного перерізу. 3) Повна перевірка міцності балки. 4) Визначення переміщень методом початкових параметрів. 5) Визначення переміщень графоаналітичним методом. 6) Визначення переміщень методом Мора.
|
Спробуй новий онлайн розрахунок прокатної балки.
1) Визначаємо опорні реакції та будуємо епюри внутрішніх зусиль.
 кН;
кН;
 кН.
кН.
Перевірка:  .
.
Побудова епюр внутрішніх зусиль (рис. 2):
Побудова епюри  (кН): (кН): Пр Пр ; ; Л Л ; ; Пр Пр ; ; Л Л ; ; Пр Пр ; ; Л Л ; ; |
Побудова епюри  (кН·м): (кН·м):  ; ;  ; ;  ; ;  ; ; |
Максимальні значення зусиль:
 кН (при
кН (при  м);
м);
 кН·м (при
кН·м (при  м).
м).
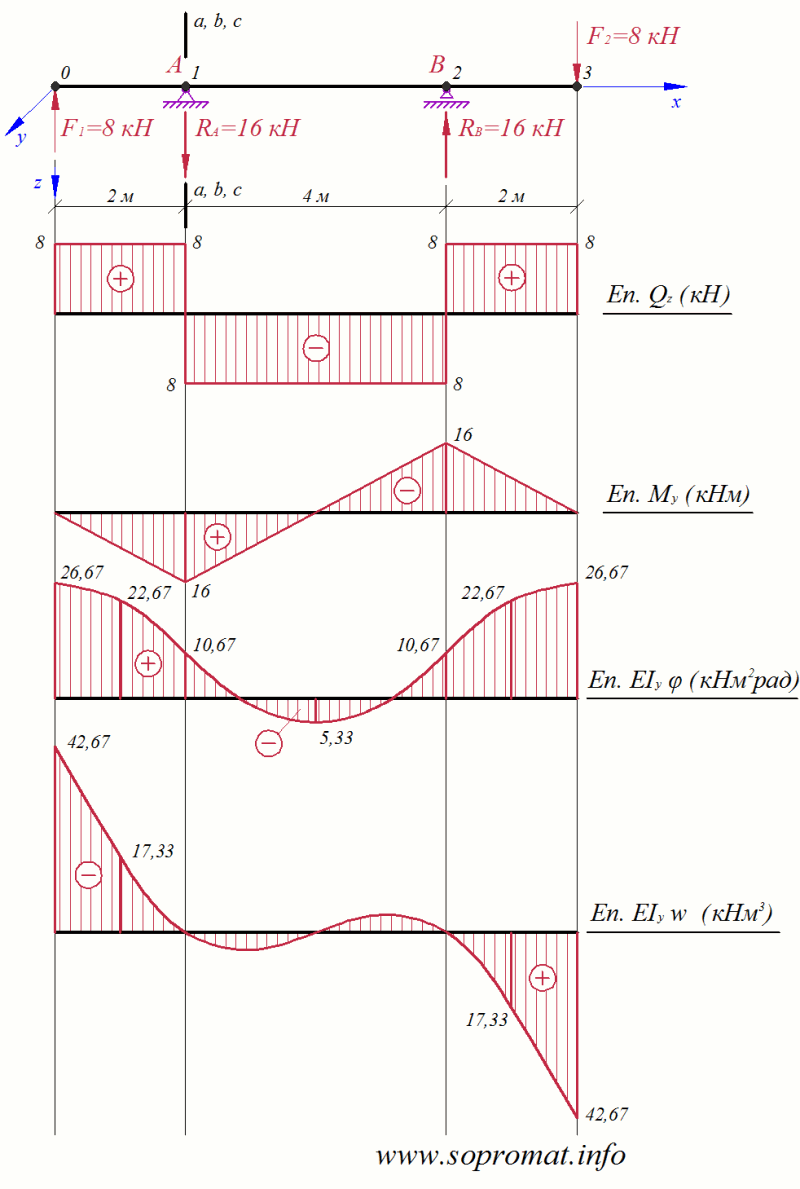
Рис. 2
2) Підбір поперечного перерізу.
Потрібний момент опору:
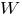 пот
пот м 3
м 3 см 3.
см 3.
З таблиці сортаменту (ГОСТ 8239-72) приймаємо двотавр №16, з такими геометричними характеристиками:
 см 4;
см 4;  см 3;
см 3;  см 3.
см 3.
Розміри перерізу:
 мм;
мм;  мм;
мм;  мм;
мм;  мм.
мм.
3) Виконуємо повну перевірку міцності балки.
а) По максимальним нормальним напруженням (переріз 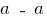 при
при  м).
м).
 Па
Па МПа.
МПа.
Недонапруження:  .
.
Для перерізу 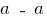 будуємо епюру нормальних напружень (рис. 3).
будуємо епюру нормальних напружень (рис. 3).
б) По максимальним дотичним напруженням (переріз 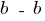 при
при  м).
м).
 Па
Па МПа.
МПа.
Недонапруження:  .
.
Обчислюємо статичний момент полки двотавра відносно центральної осі 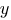 :
:
 см 3,
см 3,
дотичне напруження в точці стику полиці і стінки:
 Па
Па МПа.
МПа.
Будуємо епюру дотичних напружень в перерізі 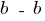 (рис. 3).
(рис. 3).
в) Головні напруження перевіряємо в (переріз 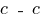 при
при  м).
м).
Зусилля в перерізі:  кН·м,
кН·м,  кН.
кН.
Визначаємо нормальне та дотичне напруження в точці стику полки та стінки двотавра:
 Па
Па МПа;
МПа;
 Па
Па МПа.
МПа.
За четвертою теорією міцності:
 МПа.
МПа.
Недонапруження:  .
.
Визначаємо дотичне напруження на нейтральній осі:
 Па
Па МПа.
МПа.
та будуємо епюри  і
і  у перерізі
у перерізі 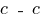 (рис. 3).
(рис. 3).
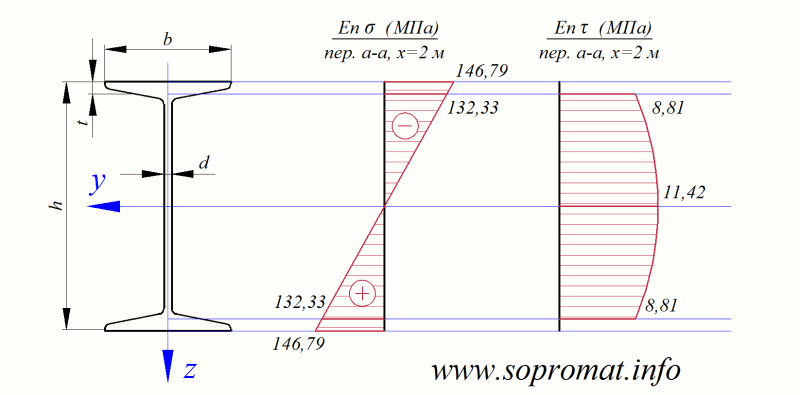
Рис. 3


 МПа,
МПа,  МПа.
МПа.