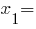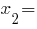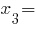Статьи

Для студента

Онлайн расчеты

Реклама

Главная » Онлайн расчет » Онлайн решение кубического уравнения 048

Онлайн решение кубического уравнения 048

Кубическое уравнение - это уравнение вида 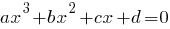ax^3 + bx^2 + cx + d = 0, где a<>0.

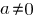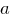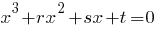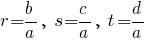После деления на a уравнение принимает канонический вид x^3 + rx^2 + sx + t = 0, где r=b/a , ~ s=c/a , ~ t=d/a.

Делая замену неизвестного 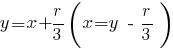y= x + r/3 (x= y ~-~ r/3), получаем так называемое приведенное уравнение:
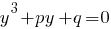y^3 + py + q = 0, где
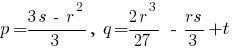p= {3s~-~r^2}/3 , ~ q= {2r^3}/27 ~-~ {rs}/3 + t.

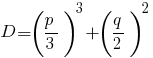Дискриминант кубического уравнения : D = (p/3)^3 + (q/2)^2.

Эсли:
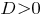D > 0 - то уравнение имеет один действительный корень и два комплексных;
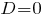D = 0 - то все корни уравнения являются действующими числами, причем по крайней мере два из них одинаковы;
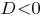D< 0 - то все три корня уравнения являются различными действительными числами;

Для нахождения решения кубического уравнения онлайн, укажите его коэффициенты и нажмите кнопку посчитать.

x^3 + x^2 + x + ~=0

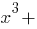
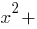
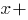
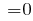
Дискриминант кубического уравнения:

D =

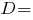
Внимание! Дискриминант слишком большой, точность расчета не гарантируется! Дискриминант больше нуля, уравнение имеет один действительный корень и два комплексных. Дискриминант равен нулю, все корни уравнения являются действующими числами, причем по крайней мере два из них одинаковы. Дискриминант меньше нуля, все три корня уравнения являются различными действительными числами.

Корни кубического уравнения:

x_1 =

x_2 =

x_3 =

Понравилась статья! Поддержи проект! Ставь ЛАЙК!