Подробное построение эпюр усилий в балке 023
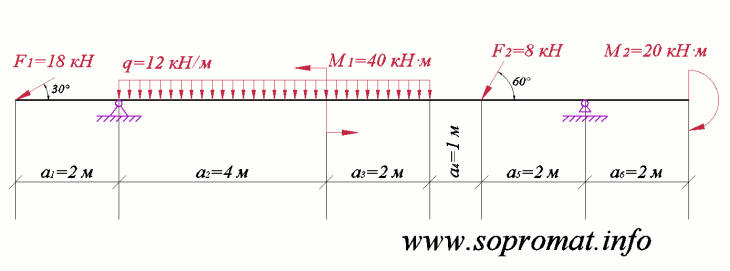
Рис. 1
Дано расчетную схему двухопорной балки (рис. 1) и приложенную к ней внешнюю нагрузку.
Нужно:
1) Определить опорные реакции.
2) Построить эпюры внутренних усилий: эпюру продольных сил (рис. 2, в), поперечных сил (рис. 2, г) и изгибающих моментов (рис. 2, д).
Решение
1) Определение опорных реакций.
Спроектируем силы 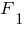 и
и 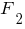 на ось
на ось  и
и 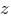 (рис. 2, а, б).
(рис. 2, а, б).
Их проекции равны:
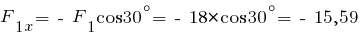 кН;
кН;
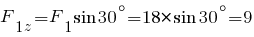 кН;
кН;
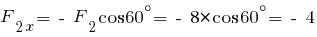 кН;
кН;
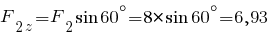 кН.
кН.
Положительный знак проекции указывает, что ее направление совпадает с положительным направлением соответствующей оси, минус - проекция направлена в отрицательную сторону оси.
На расчетной схеме балки (которая изображена на рис. 2, а) отбрасываем опорные шарниры и заменяем их реакциями в вязях (рис. 2, б). Обозначаем опоры точками 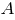 и
и 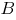 , а соответствующие реакции
, а соответствующие реакции 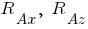 и
и 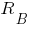 . Направление реакций выбираем произвольно, если с уравнений равновесия получим реакцию с отрицательным знаком, то ее начальное направление нужно изменить на противоположное. Используя уравнение статического равновесия (сумма проекций всех сил на оси
. Направление реакций выбираем произвольно, если с уравнений равновесия получим реакцию с отрицательным знаком, то ее начальное направление нужно изменить на противоположное. Используя уравнение статического равновесия (сумма проекций всех сил на оси  и
и 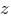 равна нулю и сумма моментов всех сил относительно любой точки равна нулю), определяем опорные реакции:
равна нулю и сумма моментов всех сил относительно любой точки равна нулю), определяем опорные реакции:
Сумма проекций на ось  :
:
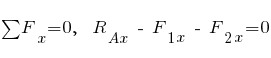 ;
;
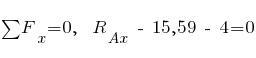 ;
;
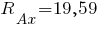 кН.
кН.
Сумма моментов всех сил относительно точки 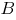 :
:
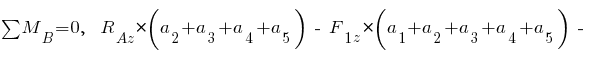
 ;
;
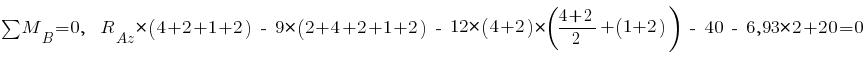 ;
;
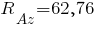 кН.
кН.
Сумма моментов всех сил относительно точки 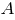 :
:
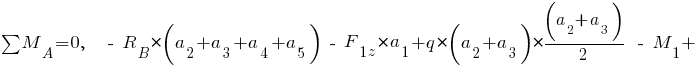
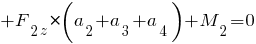 ;
;
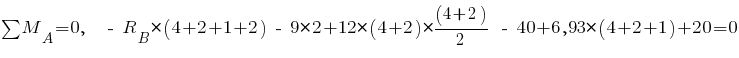 ;
;
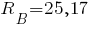 кН.
кН.
Проверка (сумма проекций всех сил на ось 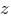 ):
):
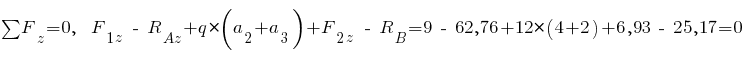 .
.
Найденные реакции обозначаем на рис. 2,б.
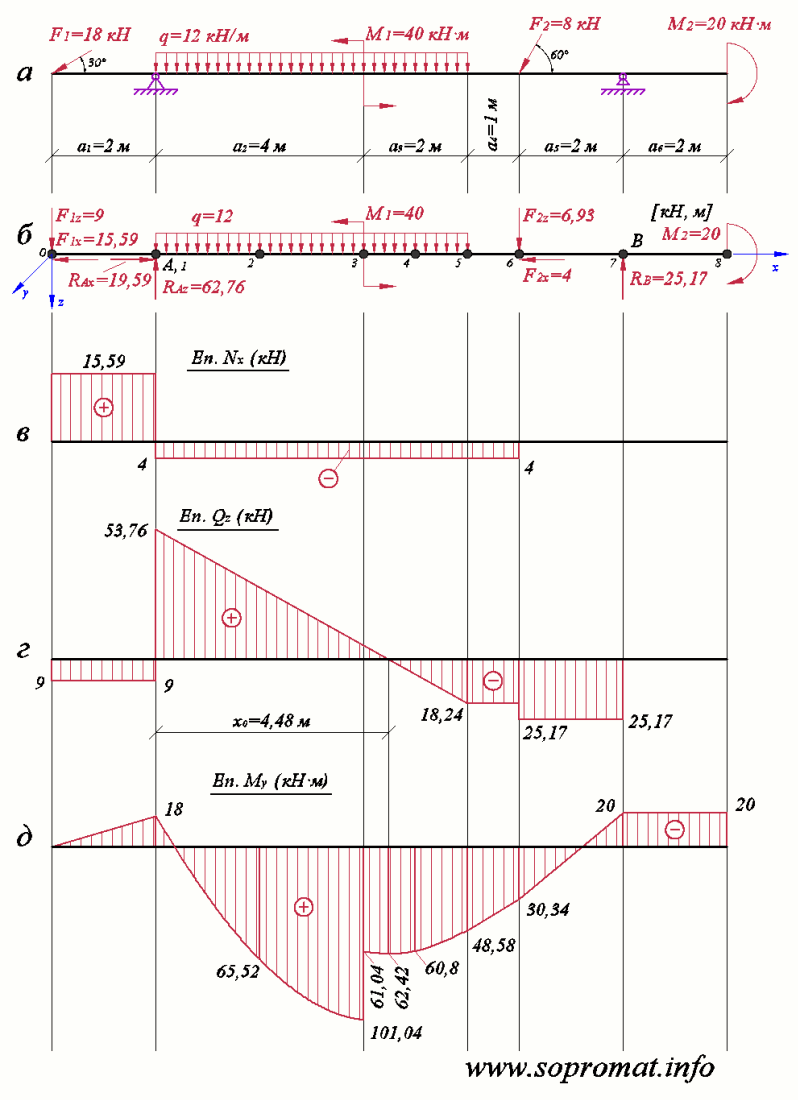
Рис. 2
2) Построение эпюр усилий.
Для нахождения внутренних усилий в характерных точках балки (начало и конец балки, точки приложения сосредоточенных сил и моментов, начало и конец равномерно распределенной нагрузки) будем использовать следующее правило знаков для построения эпюр внутренних усилий. Усилия определяются не в точке, а бесконечно близко к ней (для балки - это левое и правое сечение от характерной точки).
Определение усилий в точке "0"
• Правое сечение (рис. 3).
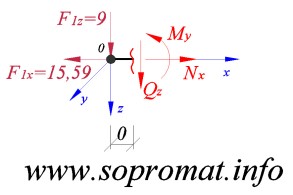
Рис. 3
Как видно из рис. 3, справа от точки "0" балка разделена на две части (левую, которая изображена на рис. 3 и правую, которую мы отбросили). Это сечение находится бесконечно близко к точке "0", то есть можно принять, что расстояние между сечением и точкой равно нулю. Для плоской задачи в поперечном сечении будут действовать три усилия (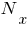 - продольная сила,
- продольная сила,  - поперечная сила и
- поперечная сила и  - изгибающий момент). Все усилия направляем так, чтобы они имели положительное направление (в соответствии с правилом знаков).
- изгибающий момент). Все усилия направляем так, чтобы они имели положительное направление (в соответствии с правилом знаков).
Для определения усилия 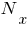 , спроектируем все силы на ось
, спроектируем все силы на ось  :
:
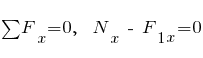 ;
;
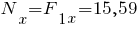 кН.
кН.
Откладываем значение усилия на рис. 2, в.
Определяем усилия  , проектируем все силы на ось
, проектируем все силы на ось 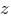 :
:
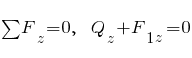 ;
;
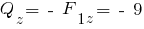 кН.
кН.
Откладываем значение усилия на рис. 2, г.
Усилие  , берем сумму моментов всех сил относительно сечения (момент, который вращается вокруг сечения против часовой стрелки, берем со знаком плюс, а по часовой стрелке - со знаком минус):
, берем сумму моментов всех сил относительно сечения (момент, который вращается вокруг сечения против часовой стрелки, берем со знаком плюс, а по часовой стрелке - со знаком минус):
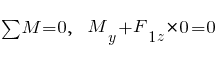 ;
;
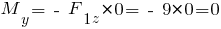 .
.
Момент относительно точки, от силы, которая проходит через эту точку, равен нулю.
Откладываем значение усилия на рис. 2, д.
В сечении где приложена сосредоточенная продольная сила, на эпюре 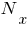 будет скачок на величину этой силы. Поэтому в таких сечениях значение продольной силы находят слева и справа от точки.
будет скачок на величину этой силы. Поэтому в таких сечениях значение продольной силы находят слева и справа от точки.
В сечении где приложена сосредоточенная поперечная сила, на эпюре  будет скачок на величину этой силы. Поэтому в таких сечениях значение поперечной силы находят слева и справа от точки.
будет скачок на величину этой силы. Поэтому в таких сечениях значение поперечной силы находят слева и справа от точки.
Определение усилий в точке "1"
• Левое сечение (рис. 4).
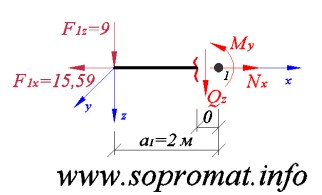
Рис. 4
Усилие 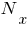 , спроектируем все силы на ось
, спроектируем все силы на ось  :
:
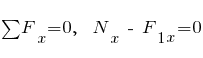 ;
;
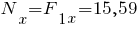 кН.
кН.
Откладываем значение усилия на рис. 2, в.
Усилие  , спроектируем все силы на ось
, спроектируем все силы на ось 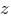 :
:
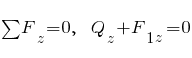 ;
;
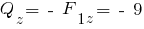 кН.
кН.
Откладываем значение усилия на рис. 2, г.
Усилие  , сумма моментов всех сил относительно сечения:
, сумма моментов всех сил относительно сечения:
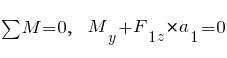 ;
;
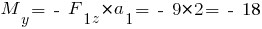 кН·м.
кН·м.
Откладываем значение усилия на рис. 2, д.
• Правое сечение (рис. 5).
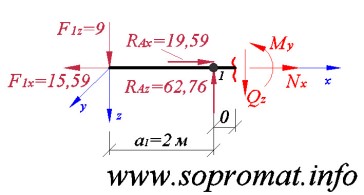
Рис. 5
Усилие 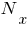 , спроектируем все силы на ось
, спроектируем все силы на ось  :
:
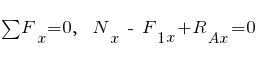 ;
;
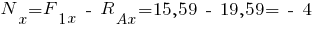 кН.
кН.
Откладываем значение усилия на рис. 2, в.
Усилие  , спроектируем все силы на ось
, спроектируем все силы на ось 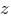 :
:
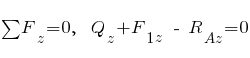 ;
;
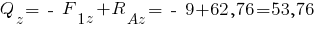 кН.
кН.
Откладываем значение усилия на рис. 2, г.
Усилие  , сумма моментов всех сил относительно сечения:
, сумма моментов всех сил относительно сечения:
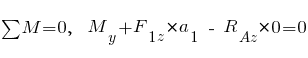 ;
;
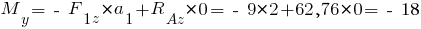 кН·м.
кН·м.
Откладываем значение усилия на рис. 2, д.
Как видим в левом и правом сечении изгибающие моменты равны. То есть в точках где приложена сосредоточенная сила и начинается (или заканчивается) равномерно распределенная нагрузка, изгибающий момент не меняется. В таких точках изгибающий момент будем находить только в одном из сечений (слева или справа от точки).
Определение усилий в точке "2"
• Левое сечение (рис. 6).
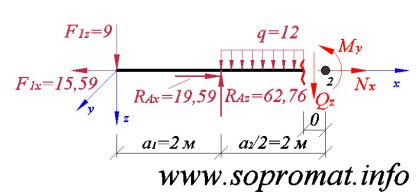
Рис. 6
Усилие 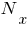 , спроектируем все силы на ось
, спроектируем все силы на ось  :
:
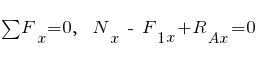 ;
;
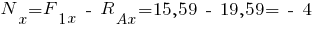 кН.
кН.
Усилие  , спроектируем все силы на ось
, спроектируем все силы на ось 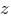 :
:
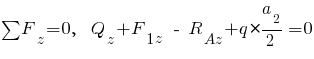 ;
;
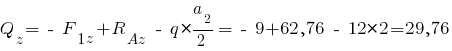 кН.
кН.
Усилие  , сумма моментов всех сил относительно сечения:
, сумма моментов всех сил относительно сечения:
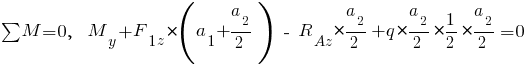 ;
;
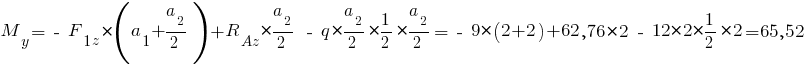 кН·м.
кН·м.
Откладываем значение усилия на рис. 2, д.
• Правое сечение (рис. 7).
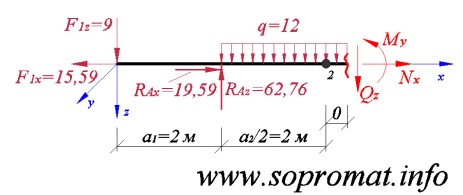
Рис. 7
Усилие 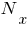 , спроектируем все силы на ось
, спроектируем все силы на ось  :
:
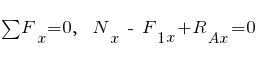 ;
;
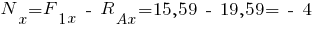 кН.
кН.
Усилие  , спроектируем все силы на ось
, спроектируем все силы на ось 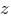 :
:
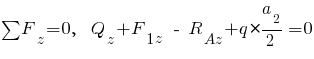 ;
;
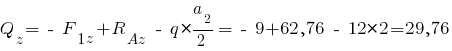 кН.
кН.
Усилие  , сумма моментов всех сил относительно сечения:
, сумма моментов всех сил относительно сечения:
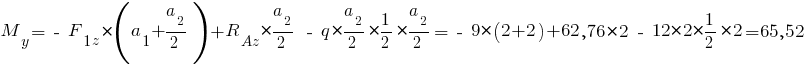 кН·м.
кН·м.
В точке "2" усилия с левой и правой стороны одинаковые. Точка "2" не характерная точка, она нужна только для нахождения изгибающего момента (под равномерно распределенной нагрузкой эпюра моментов изменяется параболой) на этом участке находим минимум три значения на эпюре моментов: в начале участка (т. "1"), в центре (т . "2") и в конце (т. "3"). В точке "4" изгибающий момент будем находить только в одном из сечений (слева или справа от точки).
Усилие 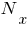 не будет меняться до точки "6", то есть в точках "3", "4" и "5" его определять не будем.
не будет меняться до точки "6", то есть в точках "3", "4" и "5" его определять не будем.
Усилие  , на участке под равномерно распределенной нагрузкой, будет изменяться прямолинейно (косой линией). Так как на участке от точки "1" до "5" нет сосредоточенных сил, то для построения эпюры поперечных сил на этом участке достаточно найти ее значение в начале (т. "1", что мы уже сделали) и в конце участка (т . "5").
, на участке под равномерно распределенной нагрузкой, будет изменяться прямолинейно (косой линией). Так как на участке от точки "1" до "5" нет сосредоточенных сил, то для построения эпюры поперечных сил на этом участке достаточно найти ее значение в начале (т. "1", что мы уже сделали) и в конце участка (т . "5").

