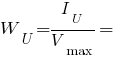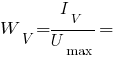Онлайн расчет геометрических характеристик сечения 046

Инструкция

Программа для проверки расчетных работ. Может работать оффлайн (загрузите эту страницу в браузер не обновляйте). Это полностью аналитический расчет, поэтому перед тем как вводить данные элементов, нужно определить координаты их центров тяжести в глобальных осях (в осях относительно которых ищется центр тяжести).

Дальнейшие инструкции будут показаны на примере сечения из трех элементов.

Выбираем количество элементов в сечении. Для данного сечения их три.

Координаты центров тяжести элементов сечения (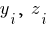). В нашем примере данные берем отсюда.
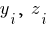y_i ,~ z_i - это координаты центров тяжести элементов сечения в осях относительно которых определяется центр тяжести (в нашей задачи это оси прямоугольника y_1 ,~ z_1 ).
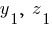Поэтому координаты первого элемента (прямоугольника) в начальных осях - (0;0) ,
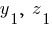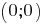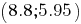второго (двутавра) - (8.8;5.95) ,
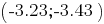третьего (уголка) - (-3.23;-3.43) .

Площадь и моменты инерции (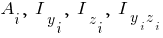 $A_i, ~I_y_i , ~I_z_i , ~I_{{y_i}{z_i}}$ ). Данные берем здесь.
Первый элемент:
A_1=32
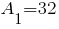
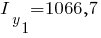
I_y_1=1066,7
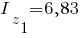
I_z_1=6,83
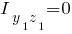
$I_{{y_1}{z_1}}=0$
Второй элемент:
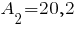
A_2=20,2
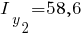
I_y_2=58,6
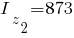
I_z_2=873
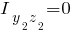
$I_{{y_2}{z_2}}=0$
Третий элемент:
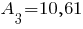
A_3=10,61
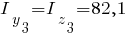
I_y_3=I_z_3=82,1
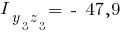
$I_{{y_3}{z_3}}= ~-~47,9$

Момент сопротивления. Пример здесь.
Есть два варианта расчета момента сопротивления.
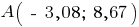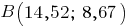Первый - внести в форму координаты самых отдаленных точек от главных осей. Для нашего примера это точка A(~-~3,08;~8,67) и B(14,52;~8,67) .
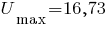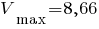Или воспользоваться вторым вариантом, указав U_max = 16,73 и V_max = 8,66 .

Результат заполнения формы расчета геометрических характеристик плоского сечения

О размерности величин.
Все геометрические характеристики должны иметь одну размерность длины (мм, см, м и тп.).
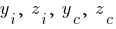y_i ,~ z_i, ~y_c ,~ z_c - размерность длины;
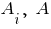A_i, ~A - длина в квадрате;
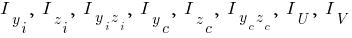$I_y_i , ~I_z_i , ~I_{{y_i}{z_i}} , ~I_y_c , ~I_z_c , ~I_{{y_c}{z_c}} , ~I_U , ~I_V$ - длина в четвертом степени;
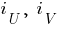- размерность длины;
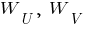W_U , ~W_V - длина в третьей степени.

Количество элементов в сечении:

№

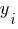
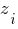
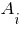
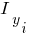
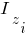
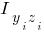
$I_{y_i z_i}$

Ошибка! Общая площадь сечения не может быть отрицательной или равной нулю.

Ошибка! В результате расчетов главный момент инерции Iyc отрицательный или равен нулю. Проверьте правильность введенных данных.

Ошибка! В результате расчетов главный момент инерции Izc отрицательный или равен нулю. Проверьте правильность введенных данных.

Ошибка! В результате расчетов главный момент инерции IU отрицательный или равен нулю. Проверьте правильность введенных данных.

Ошибка! В результате расчетов главный момент инерции Iv отрицательный или равен нулю. Проверьте правильность введенных данных.

Ошибка! Деление на ноль.

Введите данные для обчислення моментов сопротивления.

Площадь поперечного сечения:

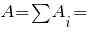
$A=sum{}{}{A_i}=$

Координаты центра тяжести сечения:

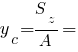
$y_c={S_z}/A=$

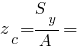
$z_c={S_y}/A=$

Моменты инерции сечения относительно центральных осей:

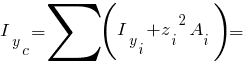
$I_y_c=sum{}{}{(I_y_i+{z_i}^2 A_i)}=$

$I_z_c=sum{}{}{(I_z_i+{y_i}^2 A_i)}=$

$I_{{y_c}{z_c}}=sum{}{}{(I_{{y_i}{z_i}}+{y_i} {z_i} A_i)} =$

Положение главных центральных осей инерции (в градусах):

$tg2{alpha_0}={2I_{{y_c}{z_c}}}/{I_z_c~-~I_y_c}$

alpha_0=

Главные центральные моменты инерции:

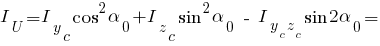
$I_U={I_y_c}cos^2{alpha_0}+{I_z_c}sin^2{alpha_0}~-~{I_{{y_c}{z_c}}}sin{2{alpha_0}}=$

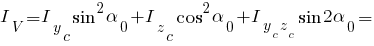
$I_V={I_y_c}sin^2{alpha_0}+{I_z_c}cos^2{alpha_0}+{I_{{y_c}{z_c}}}sin{2{alpha_0}}=$

Главные радиусы инерции:

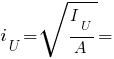
$i_U=sqrt{{I_U}/{A}}=$

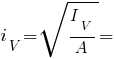
$i_V=sqrt{{I_V}/{A}}=$

Введите данные для определения момента сопротивления:

Точки	y	z
точка A			т.А - наиболее удаленная точка от оси U
точка B			т.B - наиболее удаленная точка от оси V
или введите расстояния до самых отдаленных точек
Umax=		Vmax=

Главные моменты сопротивления:

$W_U = {I_U}/{V_max} =$

$W_V = {I_V}/{U_max} =$

Понравилась статья! Поддержи проект! Ставь ЛАЙК!

Для студента

Онлайн расчеты

Реклама

Онлайн расчет геометрических характеристик сечения 046