Прокатная балка онлайн 052
Программа позволяет определить опорные реакции, построить эпюры внутренних усилий (поперечных сил, изгибающих моментов) и эпюры перемещений (угла поворота, прогиб балки) для двухопорном и консольной балки.
Дальнейшие инструкции будут приведены на примере балки на двух опорах.
1. Выберите условия крепления концов балки. Возможны варианты - свободный, шарнир и жесткое. В нашем примере левый - "шарнир", а правый - "свободный".
Если по ошибке был выбран другой вариант, нажимаем на кнопку "Новая схема".
2. Указываем длину балки, координаты опор и допускаемые напряжения. Длина балки равна "16" (м), а координаты опор от левого конца балки, соответственно к опоре A - "0" (не нужно указывать) и к опоре B - "11" (м). Допустимые нормальные напряжения σadm = 160 МПа, допустимые касательные напряжения τadm = 100 МПа.
3. Указываем нагрузки.
Выбираем количество сосредоточенных моментов - "1". В таблице вводим значения моментов и их координаты от левого конца балки. M1=18 (кН·м), a1=9 (м)(момент который вращается против часовой стрелки
- положительный, по - отрицательный).
Выбираем количество сосредоточенных сил - "1". В таблице вводим значение сил и их координаты. F1=-20 (кН), b1=4 (м) (сила направленная вниз - положительная, вверх - отрицательная).
Выбираем количество равномерно распределенной нагрузки - "1". В таблице вводим значение РРН, координаты начала и конца РРН. q1=4 (кН/м), c1=11 (м) та d1=16 (м) (РРН направлено вниз
- положительное, вверх - отрицательное).
4. Нажимаем на кнопку "Посчитать прокатную балку". После нажатия определяются опорные реакции, строятся эпюры усилий, перемещений и подбирается двутавровое сечение. Если нужно определить усилия и перемещения в произвольном сечении, введите координату в форму. Если нужно, задайте точность расчета и выберите правое или левое сечение.
Скриншот к примеру:

Скриншот к примеру (эпюра поперечных сил):

Скриншот к примеру (эпюра изгибающих моментов):

Скриншот к примеру (эпюра углов поворота):

Скриншот к примеру (эпюра прогибов):

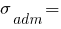 (МПа)
(МПа)
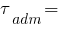 (МПа)
(МПа)
| № |
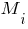
|
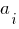
|
| № |
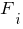
|
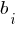
|
| № |
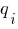
|
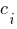
|
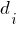
|
RA=
RB=
Координата x=
Значение эпюры Q при x=
Значение эпюры M при x=
Значение эпюры
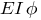 при x=
при x=
Значение эпюры
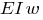 при x=
при x=
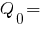 кН
кН
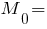 кН·м
кН·м
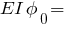 кН·м²·рад
кН·м²·рад
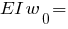 кН·м³
кН·м³
Нужный момент сопротивления:
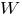 тр
тр
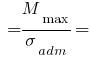 см 3
см 3
Из таблицы сортамента (ГОСТ 8239-72) принимаем двутавр №, с такими геометрическими характеристиками:
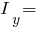 см4;
см4;
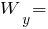 см3;
см3;
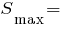 см3.
см3.
Размеры сечения:
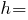 мм;
мм;
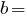 мм;
мм;
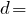 мм;
мм;
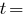 мм.
мм.
а) По максимальным нормальным напряжением (сечение
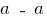 при
при
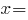 м).
м).
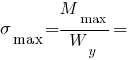 МПа
МПа
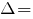 % - недонапряжение.
перенапряжение.
% - недонапряжение.
перенапряжение.
б) По максимальным касательным напряжением (сечение
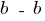 при
при
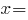 м).
м).
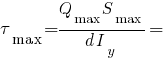 МПа
МПа
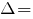 % - недонапряжение.
перенапряжение.
% - недонапряжение.
перенапряжение.
Вычисляем статический момент полки двутавра относительно центральной оси
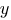 :
:
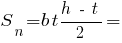 см3,
см3,
касательное напряжение в точке стыка полки и стенки:
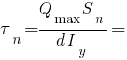 МПа.
МПа.
в) Главные напряжения проверяем в (сечение
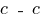 при
при
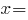 м,
).
м,
).
Усилия в сечении:
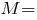 кН·м,
кН·м,
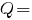 кН.
кН.
Определяем нормальное и касательное напряжение в точке стыка полки и стенки двутавра:
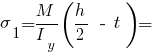 МПа;
МПа;
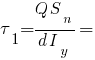 МПа.
МПа.
По четвертой теории прочности:
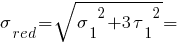 МПа
МПа
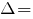 % - недонапряжение.
перенапряжение.
% - недонапряжение.
перенапряжение.
Определяем касательное напряжение на нейтральной оси:
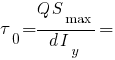 МПа.
МПа.

