Подробное построение эпюр усилий в балке 023

Определение усилий в точке "3"

• Левое сечение (рис. 8).

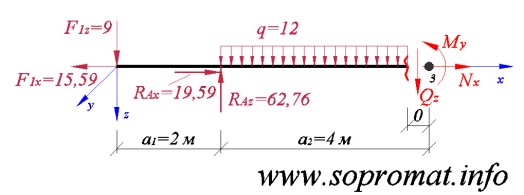
Рис. 8

Усилие , сумма моментов всех сил относительно сечения:
;
кН·м.
Откладываем значение усилия на рис. 2, д.

• Правое сечение (рис. 9).

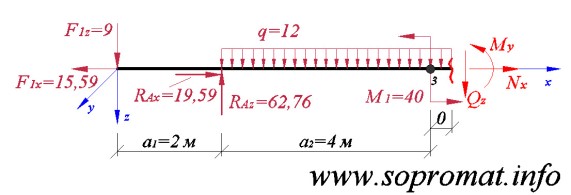
Рис. 9

Усилие , сумма моментов всех сил относительно сечения:
;
кН·м.
Откладываем значение усилия на рис. 2, д.

В сечении где приложен сосредоточенный изгибающий момент, на эпюре будет скачок на величину этого момента. Поэтому в таких сечениях значение изгибающего момента находят слева и справа от точки.

Определение усилий в точке "4"

• Правое сечение (рис. 10).

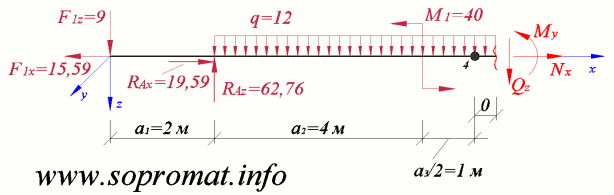
Рис. 10

Усилие , сумма моментов всех сил относительно сечения:
;
кН·м.
Откладываем значение усилия на рис. 2, д.

Определение усилий в точке "5"

• Левое сечение (рис. 11).

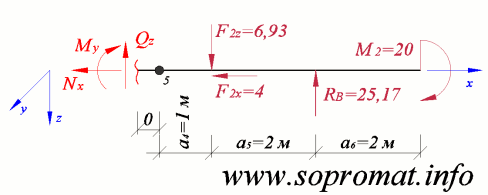
Рис. 11

Усилие , спроектируем все силы на ось :
;
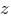кН.

Усилие , сумма моментов всех сил относительно сечения:
;
кН·м.
Откладываем значение усилия на рис. 2, д.

Определение усилий в точке "6"

• Левое сечение (рис. 12).

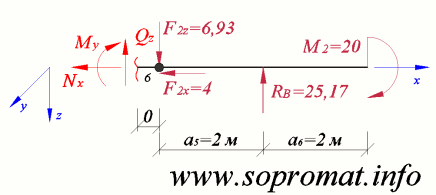
Рис. 12

Усилие 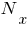, спроектируем все силы на ось :
;
кН.
Откладываем значение усилия на рис. 2, в.

Усилие , спроектируем все силы на ось :
;
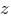кН.

Откладываем значение усилия на рис. 2, г.

Усилие , сумма моментов всех сил относительно сечения:
;
кН·м.
Откладываем значение усилия на рис. 2, д.

• Правое сечение (рис. 13).

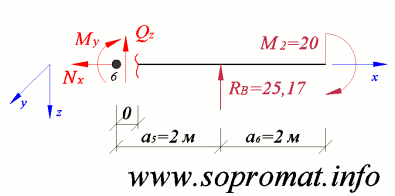
Рис. 13

Усилие 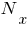, спроектируем все силы на ось :
;

Усилие , спроектируем все силы на ось :
;
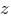кН.

Откладываем значение усилия на рис. 2, г.

Определение усилий в точке "7"

• Левое сечение (рис. 14).

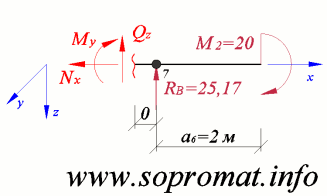
Рис. 14

Усилие , спроектируем все силы на ось :
;
кН.

Откладываем значение усилия на рис. 2, г.

Усилие , сумма моментов всех сил относительно сечения:
;
кН·м.
Откладываем значение усилия на рис. 2, д.

• Правое сечение (рис. 15).

Рис. 15

Усилие , спроектируем все силы на ось :
;
.

Откладываем значение усилия на рис. 2, г.

Определение усилий в точке "8"

• Левое сечение (рис. 16).

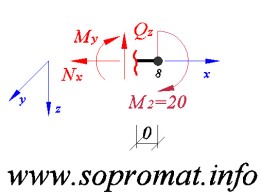
Рис. 16

Усилие , сумма моментов всех сил относительно сечения:
;
кН·м.
Откладываем значение усилия на рис. 2, д.

Определение изгибающего момента в вершине параболы (рис. 17)

Вершина параболы находится в точке где (между эпюрами и существуют дифференциальные зависимости, - это производная от , а там где производная равна нулю функция обретает экстремальное значение). Координату этой точки легко найти по формуле:

кН.

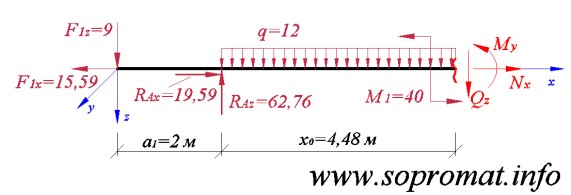
Рис. 17

Усилие , сумма моментов всех сил относительно сечения:
;
кН·м.
Откладываем значение усилия на рис. 2, д.

После построения эпюр усилий, рекомендуется проверять правильность их построения. Для этого используются дифференциальные зависимости между эпюрами та . Вот основные зависимости между этими эпюрами:

1) На участке стержня, где есть равномерно распределенная нагрузка (далее РРН):
• эпюра изменяется функцией косой линии;
• эпюра - параболой.

2) На участке стержня, где нет РРН:
• эпюра параллельная базе или равна константе (база - самая толстая линия на эпюре от которой откладываются ординаты эпюры);
• эпюра - изменяется функцией косой линии.

3)Изменение знака эпюры :
• там где - эпюра растет;
• там где - эпюра спадает;.

4) В сечении где эпюра обретает экстремальное значение.

5) В сечении на стержне, где находится сосредоточена сила:
• на эпюре будет скачок на величину этой силы (если двигаться слева направо, то скачок будет в направлении силы);
• на эпюре - злом в направлении действия силы.

6) В сечении на стержне, где находится сосредоточенный момент:
• на эпюре ничего не происходит;
• на эпюре будет скачок на величину этого момента.