Геометрические характеристики плоского поперечного сечения 3 элемента (полоса, двутавр, уголок) 018

Рис. 1 |
Дано схему поперечного сечения, составленную из трех элементов (рис. 1). Определить геометрические характеристики составного сечения. Площадь, центр тяжести, положение главных осей, главные моменты инерции, главные радиусы инерции, главные моменты сопротивления и построить эллипс инерции.
План выполнения задачи: |
1) Выписываем из таблицы сортамента (ГОСТ 8239-72 и ГОСТ 8509-86) необходимые геометрические характеристики для двутавра, уголка и вычисляем по формулам прямоугольника:
а) Полоса (прямоугольник) 200Х16
 |
 см 2, см 2, см 4, см 4, см 4, см 4, |
б) Двутавр №16
 |
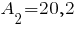 см 2, см 2,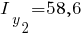 см 4, см 4,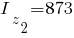 см 4, см 4,  см, см, см. см. |
в) Уголок 90Х6
 |
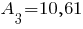 см 2, см 2,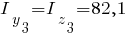 см 4, см 4, см 4, см 4,  см 4, см 4, см, см, см. см. |
2) Определяем положение центра тяжести сечения относительно начальных осей (осей полосы) 
На отдельном листе бумаги в масштабе чертим схему поперечного сечения (рис. 2) и указываем положение центральных осей каждого элемента. Выполняем привязку (указываем расстояния) центров тяжести каждого элемента относительно начальных осей 
Координаты центров тяжести элементов в осях 

 см,
см,
 см,
см,

 см,
см,
 см.
см.

Рис. 2
Площадь поперечного сечения:
 см 2,
см 2,
Координаты центра тяжести сечения:
 см,
см,
 см.
см.
Откладываем на рисунке координаты  и
и  с учетом знаков, обозначаем положение центра тяжести (точка С) и проводим центральные оси
с учетом знаков, обозначаем положение центра тяжести (точка С) и проводим центральные оси 
Контролируем достоверность определения положения центра тяжести сложного сечения. Для этого вычисляем координаты центров тяжести элементов сечения в координатных осях  и
и  (расстояния между собственными центральными осями отдельных элементов и центральными осями сечения):
(расстояния между собственными центральными осями отдельных элементов и центральными осями сечения):
|
|
|
и статические моменты площади сечения относительно центральных осей:
 см 3,
см 3,
погрешность: 
 см 3,
см 3,
погрешность: 
3) На основании формул параллельного перехода вычисляем моменты инерции сечения относительно центральных осей  и
и 
- осевые

 см 4,
см 4,

 см 4,
см 4,
- центробежный

 см 4.
см 4.
4) Определяем положение главных центральных осей инерции:

Отсюда 
На рисунке откладываем положительный угол против часовой стрелки и чертим главные центральные оси инерции (рис. 3).
5) Для определения величин главных центральных моментов инерции используем три вида формул.
а)

 см 4,
см 4,

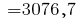 см 4,
см 4,
Для проверки правильности нахождения главных моментов инерции, определяем центробежный момент инерции относительно главных осей:

 ,
,
погрешность: 
б)
 см 4,
см 4,
 см 4,
см 4,
в)

 .
.
Поскольку  , то
, то 
 см 4,
см 4,
 см 4.
см 4.
Проверяем условие инвариантности осевых моментов инерции:

 см 4,
см 4,
 см 4.
см 4.
6) Вычисляем главные радиусы инерции:
 см,
см,
 см,
см,
и строим эллипс инерции (рис. 3). Определяем графически радиусы инерции относительно осей 
 см,
см, см.
см.
Вычисляем моменты инерции относительно этих осей:
 см 4,
см 4,
 см 4,
см 4,
и сравниваем с ранее вычисленными значениями:
 см 4,
см 4, см 4.
см 4.
7) Определяем главные моменты сопротивления  и
и 
Наиболее удаленной точкой от оси  является точка
является точка  а от оси
а от оси  - точка
- точка  Измеряя на рисунке расстояния до этих точек от соответствующих главных осей, находим:
Измеряя на рисунке расстояния до этих точек от соответствующих главных осей, находим: 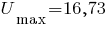 см,
см, 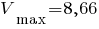 см.
см.
Проверяем по формулам:
 см,
см,
 см.
см.
Главные моменты сопротивления:
 см 3,
см 3,
 см 3.
см 3.

Рис. 3



 см,
см, см,
см, см.
см.
 см,
см, см,
см, см.
см.