Метод начальных параметров (изгиб стержня) 016

Рис. 1
Угол поворота сечения на расстоянии  от начала координат:
от начала координат:

![~+ sum{i}{~}{q_i /6 delim{[}{(x~-~c_i)^3 -~ (x~-~d_i)^3}{]}}](/image/formula/math_959_599226ad14243cfddfe4a6b66d61a4c0.png) ;
;
Прогиб на расстоянии  от начала координат:
от начала координат:

![+ sum{i}{~}{q_i /24 delim{[}{(x~-~c_i)^4 -~ (x~-~d_i)^4}{]}}](/image/formula/math_959_7dcf20f61670c416c864ce0bb1737463.png) ;
;
Начало координат находится на левом конце стержня, ось  направлена вправо.
направлена вправо.
Здесь  - расстояние от начала координат до сечения, в котором определяются угол поворота и прогиб стержня.
- расстояние от начала координат до сечения, в котором определяются угол поворота и прогиб стержня.
 - начальные параметры (прогиб, угол поворота, изгибающий момент и поперечная сила в начале стержня (с левой стороны стержня).
- начальные параметры (прогиб, угол поворота, изгибающий момент и поперечная сила в начале стержня (с левой стороны стержня).
 - соответственно расстоянию от начала стержня до сечений, в которых приложены сосредоточенные момент
- соответственно расстоянию от начала стержня до сечений, в которых приложены сосредоточенные момент 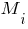 , сила
, сила 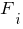 , начинается и заканчивается действие равномерно распределенной нагрузки
, начинается и заканчивается действие равномерно распределенной нагрузки 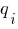 (рис. 1).
(рис. 1).
 - изгибная жесткость стержня.
- изгибная жесткость стержня.
Перемещение, вычисленные по приведенным формулам, получаем увеличенными в  раз. Для определения перемещений нужно, чтобы, помимо внешних нагрузок, были известны все начальные параметры. Начальные усилия
раз. Для определения перемещений нужно, чтобы, помимо внешних нагрузок, были известны все начальные параметры. Начальные усилия  берутся равными ординатам эпюр
берутся равными ординатам эпюр  и
и  на левом конце балки. Начальные перемещения
на левом конце балки. Начальные перемещения  зависят от условий закрепления балки (рис. 2).
зависят от условий закрепления балки (рис. 2).

Рис. 2
Используя формулы перемещений, следует помнить, что в них учитываются все прилагаемые к балке внешние нагрузки (учитывая и реакции опор), которые находятся с левой стороны от рассматриваемого сечения.
Нужно также обратить внимание на знаки величин, входящих в формулы. Внешние нагрузки, имеющие направления, указанные на рис. 1, подставляются со знаком "+", при противоположном направлении любой нагрузки соответствующие составляющие формулы меняют знак на противоположный. Правило знаков для перемещений следующее: угол поворота по часовой стрелке, в прогиб вниз считаются положительными.
Между функциями  и интенсивностью нагрузки
и интенсивностью нагрузки  существуют такие дифференциальные зависимости:
существуют такие дифференциальные зависимости:
 .
.
Нужно следить, чтобы построенные эпюры отвечали приведенным зависимостям (в смысле правильного расположения точек экстремума, перегиба, нулевых точек и т.п.).

