Пример 1. Расчет прокатной балки 022
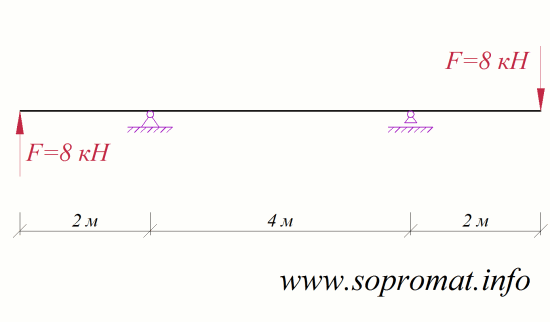
Рис. 1
|
Дано: схема балки с нагрузкой (рис. 1), допускаемые напряжения Нужно: определить опорные реакции, построить эпюры внутренних усилий, подобрать сечение балки с двутавра и проверить прочность принятого сечения, построить эпюры перемещений, методом Мора и графоаналитическим методом в произвольном сечении балки определить угол поворота и прогиб. |
План выполнения задачи: 1) Определение опорных реакций и построение эпюр внутренних усилий. 2) Подбор поперечного сечения. 3) Полная проверка прочности балки. 4) Определение перемещений методом начальных параметров. 5) Определение перемещений графоаналитическим методом. 6) Определение перемещений методом Мора.
|
Попробуй новый онлайн расчет прокатной балки.
1) Определяем опорные реакции и строим эпюры внутренних усилий.
 кН;
кН;
 кН.
кН.
Проверка:  .
.
Построение эпюр внутренних усилий (рис. 2):
Построение эпюры  (кН): (кН): Пр Пр ; ; Л Л ; ; Пр Пр ; ; Л Л ; ; Пр Пр ; ; Л Л ; ; |
Построение эпюры  (кН·м): (кН·м):  ; ;  ; ;  ; ;  ; ; |
Максимальные значения усилий:
 кН (при
кН (при  м);
м);
 кН·м (при
кН·м (при  м).
м).
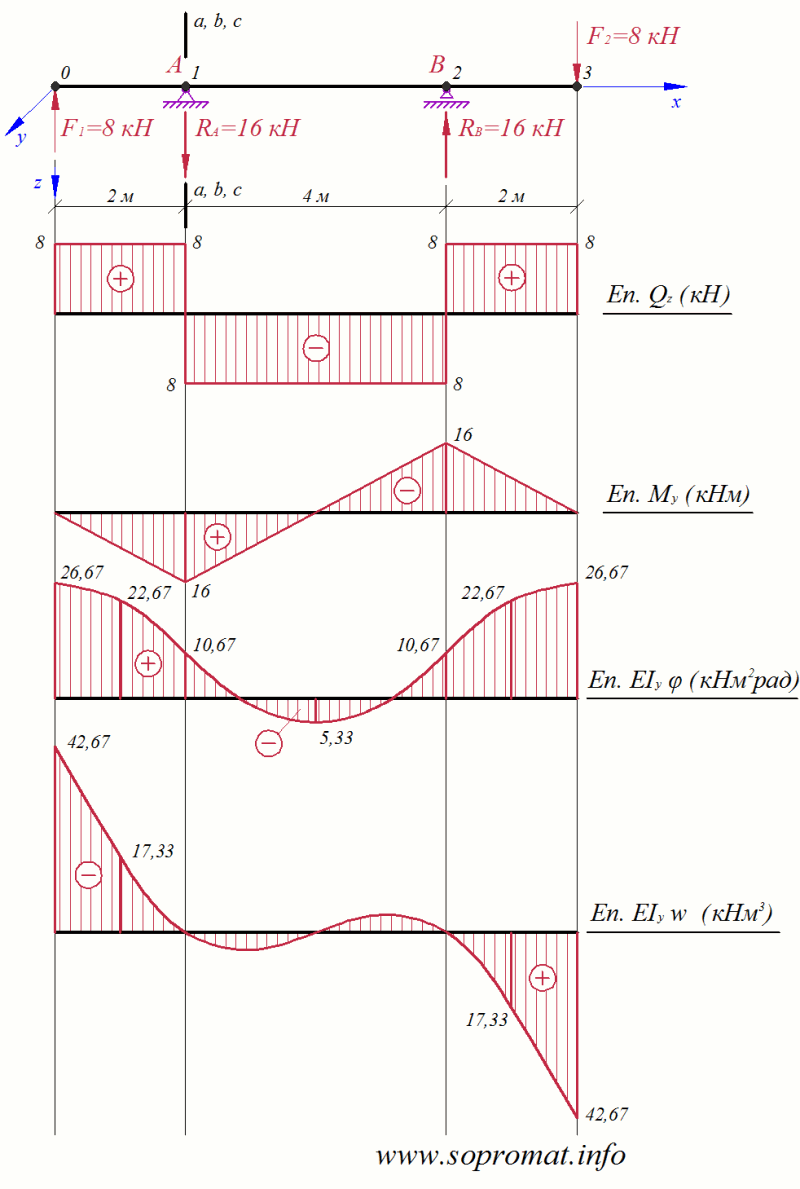
Рис. 2
2) Подбор поперечного сечения.
Требуемый момент сопротивления:
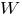 тр
тр м 3
м 3 см 3.
см 3.
Из таблицы сортамента (ГОСТ 8239-72) принимаем двутавр №16, с такими геометрическими характеристиками:
 см 4;
см 4;  см 3;
см 3;  см 3.
см 3.
Размеры сечения:
 мм;
мм;  мм;
мм;  мм;
мм;  мм.
мм.
3) Выполняем полную проверку прочности балки.
а) По максимальным нормальным напряжением (сечение 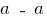 при
при  м).
м).
 Па
Па МПа.
МПа.
Недонапряжение:  .
.
Для сечения 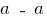 строим эпюру нормальных напряжений (рис. 3).
строим эпюру нормальных напряжений (рис. 3).
б) По максимальным касательным напряжением (сечение 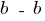 при
при  м).
м).
 Па
Па МПа.
МПа.
Недонапряжение:  .
.
Вычисляем статический момент полки двутавра относительно центральной оси 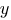 :
:
 см 3,
см 3,
касательное напряжение в точке стыка полки и стенки:
 Па
Па МПа.
МПа.
Строим эпюру касательных напряжений в сечении 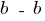 (рис. 3).
(рис. 3).
в) Главные напряжения проверяем в (сечение 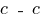 при
при  м).
м).
Усилия в сечении:  кН·м,
кН·м,  кН.
кН.
Определяем нормальное и касательное напряжение в точке стыка полки и стенки двутавра:
 Па
Па МПа;
МПа;
 Па
Па МПа.
МПа.
За четвертой теорией прочности:
 МПа.
МПа.
Недонапряжение:  .
.
Определяем касательное напряжение на нейтральной оси:
 Па
Па МПа.
МПа.
и строим эпюры  и
и  в сечении
в сечении 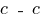 (рис. 3).
(рис. 3).
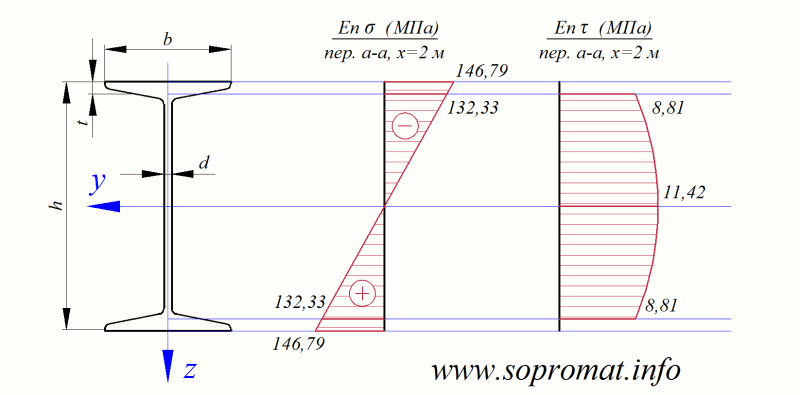
Рис. 3


 МПа,
МПа,  МПа.
МПа.