Пример 1. Определение моментов инерции относительно заданных осей (2 прокатных элемента) 021

геометрические характеристики составного поперечного сечения

Рис. 1

Дано схему поперечного сечения, составленную из двух элементов (рис. 1). Определить осевые моменты инерции и центробежный момент инерции относительно заданных осей.

План выполнения задачи:
1) Геометрические характеристики элементов сечения.
2) Определение моментов инерции относительно вспомогательных осей.
3) Определение моментов инерции относительно заданных осей.

1) Выписываем из таблицы сортамента (ГОСТ 8240-72 и ГОСТ 8509-86) необходимые геометрические характеристики для швеллера и уголка:

а) Швеллер №16

см ²,

см ⁴,

см ⁴,
$I_{{y_1}{z_1}}=0 ,$
b=6,4

см,

см.

б) Уголок 70Х10

см ²,

см ⁴,

см ⁴,
$I_{{y_2}{z_2}}= pm(I_max ~-~ I_y_3 )=$
= ~-~(91,52 ~-~ 57,9) = ~-~33,62

см ⁴,

см,

см.

2) Определяем моменты инерции относительно вспомогательных осей .

На отдельном листе бумаги в масштабе чертим схему поперечного сечения (рис. 2) и указываем положение центральных осей каждого элемента. Параллельно центральным осям элементов сечения через точку ноль проводим вспомогательные оси y_0 ,~z_0 . Выполняем привязку (указываем расстояния) центров тяжести каждого элемента относительно вспомогательных осей .

Координаты центров тяжести элементов в осях y_0 ,~z_0 :

y_01 = 16/2 = 8 см,

y_02 = 16 ~-~ 2,1 = 13,9 см,

z_01 = ~-~1,8 см,

z_02 = 7 ~-~ 2,1 = 4,9 см.

составленное сечение

Рис. 2

На основе формул параллельного перехода вычисляем моменты инерции сечения относительно вспомогательных осей y_0 та z_0 :

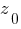- осевые моменты инерции

$I_y_0=sum{i=1}{2}{(I_y_i+{z_{0i}}^2 A_i)}= 63,3 + {(~-~1,8)}^2*18,1 + 57,9 + {4,9}^2*13,11 = 494,62$ см ⁴,

$I_z_0=sum{i=1}{2}{(I_z_i+{y_{0i}}^2 A_i)}= 747 + {8}^2*18,1 + 57,9 + {13,9}^2*13,11 = 4496,28$ см ⁴,

- центробежный момент инерции

$I_{{y_0}{z_0}}=sum{i=1}{2}{(I_{{y_i}{z_i}}+{y_{0i}} {z_{0i}} A_i)} = 0 + 8*(~-~1,8)*18,1 + (~-~33,62) + 13,9*4,9*13,11 = 598,66$ см ⁴.

3) Определяем моменты инерции относительно заданных осей .

моменты инерции при повороте осей

Рис. 3

На рис. 3 под заданным углом проводим оси y_p ,~z_p . Определяем наименьший угол alpha ~(beta) , на который нужно вернуть вспомогательные оси y_0 ,~z_0 , так чтобы они совпали с осями .

alpha = 180^circ ~-~ 20^circ = 160^circ , ~(beta = ~-~20^circ) .

Для определения моментов инерции относительно заданных осей, используем формулы определения моментов инерции при повороте координатных осей:

- осевые моменты инерции относительно искомых осей

$I_y_p={I_y_0}cos^2{alpha}+{I_z_0}sin^2{alpha}~-~{I_{{y_0}{z_0}}}sin{2{alpha}}= 494,62 cos^2{160^circ} + 4496,28 sin^2{160^circ} ~-~$
$~-~ 598,66 sin{2*160^circ} = 1347,53$ см ⁴,

$I_z_p={I_y_0}sin^2{alpha}+{I_z_0}cos^2{alpha}+{I_{{y_0}{z_0}}}sin{2{alpha}}= 494,62 sin^2{160^circ} + 4496,28 cos^2{160^circ} +$
$+ 598,66 sin{2*160^circ} = 3643,36$ см ⁴,

- центробежный момент инерции относительно искомых осей

$I_{y_p z_p} = I_{{y_0}{z_0}} cos{2alpha} + 1/2 ( I_y_0 ~-~ I_z_0 ) sin{2alpha} = 598,66 cos{2*160^circ} +$
$+ 1/2 (494,62 ~-~ 4496,28) sin{2*160^circ} = 1744,71$ .

Понравилась статья! Поддержи проект! Ставь ЛАЙК!

Для студента

Онлайн расчеты

Реклама

Пример 1. Определение моментов инерции относительно заданных осей (2 прокатных элемента) 021