Пример 3. Построение эпюр усилий в шарнирной балке 032

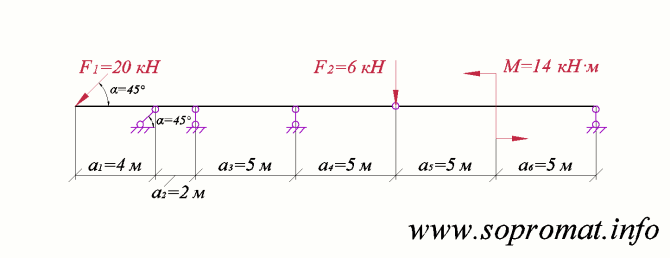
Рис. 1

Дано расчетную схему шарнирной балки (рис. 1) и приложенною к ней внешнюю нагрузку.

Нужно:
1) Определить опорные реакции.
2) Построить эпюры внутренних усилий: эпюру продольных сил (рис. 2, Еп.N_x), поперечных сил (рис. 2, Еп.Q_z) и изгибающих моментов (рис. 2, Еп.M_y).

Решение:

1) Определение опорных реакций.

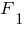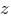Спроектируем силу на ось и (рис. 2).
Ее проекции равны:
кН;
кН.

Поскольку в сквозном шарнире изгибающий момент равен нулю, то балку, изображенную на рис.1, можно рассчитывать как две отдельные балки (рис. 2, I, II). Расчет начинаем с балки, в которой количество опорных реакций соответствует количеству уравнений статического равновесия статики (для плоских задач - три уравнения). Опорная реакция (где находится шарнир) первой балки, передается на другие балки с противоположным знаком.

I - балка

Сумма моментов всех сил относительно точки :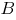
;
;
кН.

Сумма моментов всех сил относительно точки :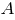
;
;
кН.

II - балка

Сумма проекций всех сил на ось :
;
;
кН.

Сумма моментов всех сил относительно точки :
Поскольку треугольник - прямоугольный равнобедренный треугольник, то м.
;
;
кН.

Сумма моментов всех сил относительно точки :
Поскольку треугольник - прямоугольный равнобедренный треугольник, то м.
;
;
кН.

Проверка (сумма проекций всех сил на ось ):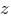
.

2) Построение эпюр внутренних усилий.

Обозначаем характерные точки и определяем в них значение усилий, используя соответствующее правило знаков для построения эпюр внутренних усилий.

Построение эпюры продольных сил (Еп.N_x, кН):
^Л;
^Пр.

Строим эпюру продольных сил (рис.2).

Построение эпюры поперечных сил (Еп.Q_z, кН):
^Л;
^Пр;
^Л;
^Пр;
^Л;
^Пр;
^Л;
^Пр;
^Л;
^Пр.

Строим эпюру поперечных сил (рис.2).

Построение эпюры изгибающих моментов (Еп.M_y, кН·м):
;
^Пр;
^Л;
;
;
;
;
.

Строим эпюру изгибающих моментов (рис.2).

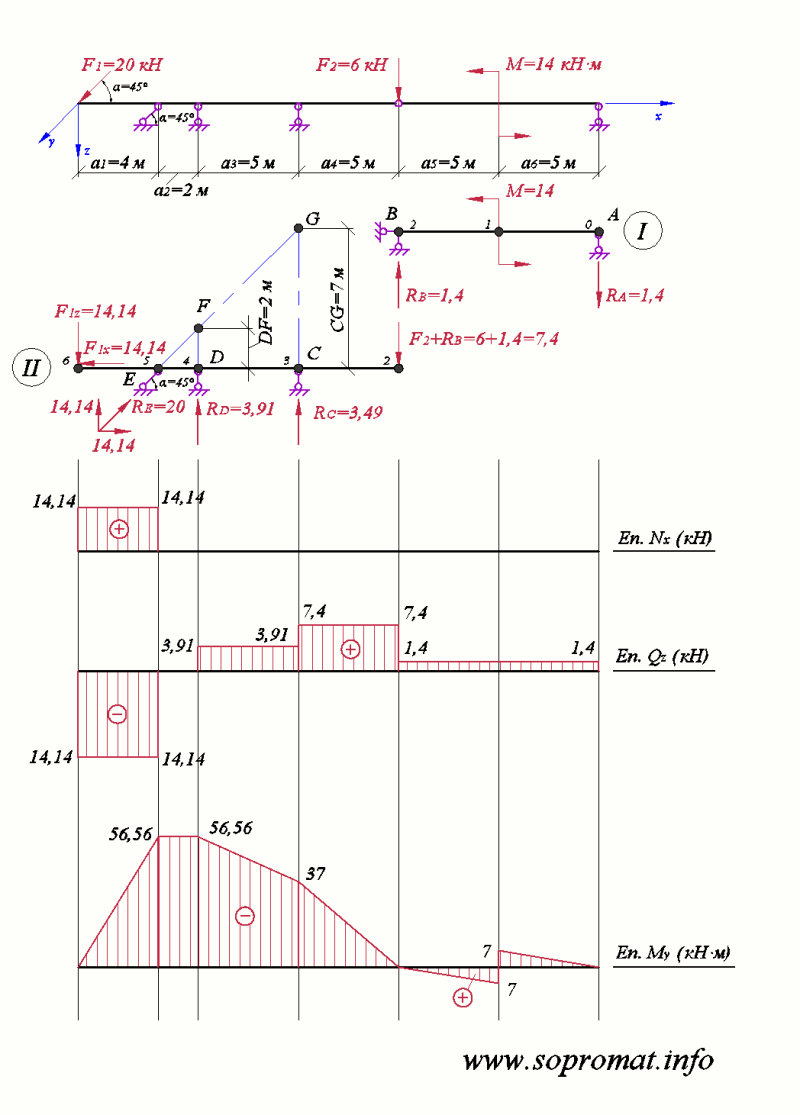
Рис. 2