Пример 3. Расчет прокатной балки 045

|< < 1 2

Показано с 2 по 2 из 2 (всего 2 страниц)

4) Вычисляем перемещения оси балки методом начальных параметров.

Начальные параметры: w_0 = ?, ~~~ phi_0 = ?, ~~~ M_0 = ~-~ 16, ~~~ Q_0 = 0 кН.

Предельные и дополнительные условия:

при x = 8 м right ~~w = 0 ;

при x = 17 м right ~~w = 0 .

Используя формулы для вычисления прогиба оси балки методом начальных параметров, запишем:

$EI_y w(8) = EI_y w_0 + EI_y phi_0 * 8 + 16 * {{8^2}/{2}} ~-~ 10 * {{(8 ~-~ 4)^3}/{6}} = 0$ ;

$EI_y w(17) = EI_y w_0 + EI_y phi_0 * 17 + 16 * {{17^2}/{2}} ~-~ 10 * {{(17 ~-~ 4)^3}/{6}} + 5,56 * {{(17 ~-~ 8)^3}/{6}} +$
$+ {{4}/{24}} * [(17 ~-~ 11)^4 ~-~ (17 ~-~ 15)^4]= 0$ .

или

EI_y w_0 + EI_y phi_0 * 8 = ~-~ 405,33 ;

EI_y w_0 + EI_y phi_0 * 17 = 460,79 .

Решая систему уравнений, находим:

EI_y w_0 = ~-~ 1175,7 кН·м ³; EI_y phi_0 = 96,3 кН·м ² рад.

Делим балку на участки и определяем значение угла поворота и прогиба в характерных точках (на границах участков и посередине каждого участка,
рис. 2).

Составляем выражения для угла поворота и прогиба для каждого участка и вычисляем значение EI_y phi и EI_y w .

Первый участок ( 0<=x<=4 м)

EI_y phi(x) = 96,3 + 16 * x ;

$EI_y w(x) = ~-~ 1175,7 + 96,3 * x + 16 * {{x^2}/{2}}$ .

x = 0

EI_y phi(0) = 96,3 кН·м ² рад;

EI_y w(0) = ~-~ 1175,7 кН·м ³.

x = 2 м

EI_y phi(2) = 96,3 + 16 * 2 = 128,3 кН·м ² рад;

$EI_y w(2) = ~-~ 1175,7 + 96,3 * 2 + 16 * {{2^2}/{2}} = ~-~ 951,11$ кН·м ³.

x = 4 м

EI_y phi(4) = 96,3 + 16 * 4 = 160,3 кН·м ² рад;

$EI_y w(4) = ~-~ 1175,7 + 96,3 * 4 + 16 * {{4^2}/{2}} = 662,52$ кН·м ³.

Второй участок ( 4<x<=8 м)

$EI_y phi(x) = 96,3 + 16 * x ~-~ 10 * {{(x ~-~ 4)^2}/{2}}$ ;

$EI_y w(x) = ~-~ 1175,7 + 96,3 * x + 16 * {{x^2}/{2}} ~-~ 10 * {{(x ~-~ 4)^3}/{6}}$ .

x = 6 м

$EI_y phi(6) = 96,3 + 16 * 6 ~-~ 10 * {{(6 ~-~ 4)^2}/{2}} = 172,3$ кН·м ² рад;

$EI_y w(6) = ~-~ 1175,7 + 96,3 * 6 + 16 * {{6^2}/{2}} ~-~ 10 * {{(6 ~-~ 4)^3}/{6}} = ~-~ 323,26$ кН·м ³.

x = 8 м

$EI_y phi(8) = 96,3 + 16 * 8 ~-~ 10 * {{(8 ~-~ 4)^2}/{2}} = 144,3$ кН·м ² рад;

$EI_y w(8) = ~-~ 1175,7 + 96,3 * 8 + 16 * {{8^2}/{2}} ~-~ 10 * {{(8 ~-~ 4)^3}/{6}} = 0$ кН·м ³.

Третий участок ( 8<x<=11 м)

$EI_y phi(x) = 96,3 + 16 * x ~-~ 10 * {{(x ~-~ 4)^2}/{2}} + 5,56 * {{(x ~-~ 8)^2}/{2}}$ ;

$EI_y w(x) = ~-~ 1175,7 + 96,3 * x + 16 * {{x^2}/{2}} ~-~ 10 * {{(x ~-~ 4)^3}/{6}} + 5,56 * {{(x ~-~ 8)^3}/{6}}$ .

x = 9,5 м

$EI_y phi(9,5) = 96,3 + 16 * 9,5 ~-~ 10 * {{(9,5 ~-~ 4)^2}/{2}} + 5,56 * {{(9,5 ~-~ 8)^2}/{2}} = 103,3$ кН·м ² рад;

$EI_y w(9,5) = ~-~ 1175,7 + 96,3 * 9,5 + 16 * {{9,5^2}/{2}} ~-~ 10 * {{(9,5 ~-~ 4)^3}/{6}} + 5,56 * {{(9,5 ~-~ 8)^3}/{6}} = 186,94$ кН·м ³.

x = 11 м

$EI_y phi(11) = 96,3 + 16 * 11 ~-~ 10 * {{(11 ~-~ 4)^2}/{2}} + 5,56 * {{(11 ~-~ 8)^2}/{2}} = 52,3$ кН·м ² рад;

$EI_y w(9,5) = ~-~ 1175,7 + 96,3 * 11 + 16 * {{11^2}/{2}} ~-~ 10 * {{(11 ~-~ 4)^3}/{6}} + 5,56 * {{(9,5 ~-~ 8)^3}/{6}} = 304,89$ кН·м ³.

Четвертый участок ( 11<x<=15 м)

$EI_y phi(x) = 96,3 + 16 * x ~-~ 10 * {{(x ~-~ 4)^2}/{2}} + 5,56 * {{(x ~-~ 8)^2}/{2}} + {{4}/{6}} * (x ~-~ 11)^3$ ;

$EI_y w(x) = ~-~ 1175,7 + 96,3 * x + 16 * {{x^2}/{2}} ~-~ 10 * {{(x ~-~ 4)^3}/{6}} + 5,56 * {{(x ~-~ 8)^3}/{6}} + {{4}/{24}} * (x ~-~ 11)^4$ .

x = 13 м

$EI_y phi(13) = 96,3 + 16 * 13 ~-~ 10 * {{(13 ~-~ 4)^2}/{2}} + 5,56 * {{(13 ~-~ 8)^2}/{2}} + {{4}/{6}} * (13 ~-~ 11)^3 = ~-~ 25,93$ кН·м ² рад;

$EI_y w(13) = ~-~ 1175,7 + 96,3 * 13 + 16 * {{13^2}/{2}} ~-~ 10 * {{(13 ~-~ 4)^3}/{6}} + 5,56 * {{(13 ~-~ 8)^3}/{6}} + {{4}/{24}} * (13 ~-~ 11)^4 = 331,56$ кН·м ³.

x = 15 м

$EI_y phi(15) = 96,3 + 16 * 15 ~-~ 10 * {{(15 ~-~ 4)^2}/{2}} + 5,56 * {{(15 ~-~ 8)^2}/{2}} + {{4}/{6}} * (15 ~-~ 11)^3 = ~-~ 89,93$ кН·м ² рад;

$EI_y w(15) = ~-~ 1175,7 + 96,3 * 15 + 16 * {{15^2}/{2}} ~-~ 10 * {{(15 ~-~ 4)^3}/{6}} + 5,56 * {{(15 ~-~ 8)^3}/{6}} + {{4}/{24}} * (15 ~-~ 11)^4 = 210,67$ кН·м ³.

Пятый участок ( 15<x<=17 м)

$EI_y phi(x) = 96,3 + 16 * x ~-~ 10 * {{(x ~-~ 4)^2}/{2}} + 5,56 * {{(x ~-~ 8)^2}/{2}} + {{4}/{6}} * [(x ~-~ 11)^3 ~-~ (x ~-~ 15)^3]$ ;

$EI_y w(x) = ~-~ 1175,7 + 96,3 * x + 16 * {{x^2}/{2}} ~-~ 10 * {{(x ~-~ 4)^3}/{6}} + 5,56 * {{(x ~-~ 8)^3}/{6}} + {{4}/{24}} * [(x ~-~ 11)^4 ~-~ (x ~-~ 15)^4]$ .

x = 16 м

$EI_y phi(16) = 96,3 + 16 * 16 ~-~ 10 * {{(16 ~-~ 4)^2}/{2}} + 5,56 * {{(16 ~-~ 8)^2}/{2}} +$
$+ {{4}/{6}} * [(16 ~-~ 11)^3 ~-~ (16 ~-~ 15)^3]= ~-~ 107,26$ кН·м ² рад;

$EI_y w(16) = ~-~ 1175,7 + 96,3 * 16 + 16 * {{16^2}/{2}} ~-~ 10 * {{(16 ~-~ 4)^3}/{6}} + 5,56 * {{(16 ~-~ 8)^3}/{6}} +$
$+ {{4}/{24}} * [(16 ~-~ 11)^4 ~-~ (16 ~-~ 15)^4]= 111,11$ кН·м ³.

x = 17 м

$EI_y phi(17) = 96,3 + 16 * 17 ~-~ 10 * {{(17 ~-~ 4)^2}/{2}} + 5,56 * {{(17 ~-~ 8)^2}/{2}} +$
$+ {{4}/{6}} * [(17 ~-~ 11)^3 ~-~ (17 ~-~ 15)^3]= ~-~ 113,04$ кН·м ² рад;

$EI_y w(17) = ~-~ 1175,7 + 96,3 * 17 + 16 * {{17^2}/{2}} ~-~ 10 * {{(17 ~-~ 4)^3}/{6}} + 5,56 * {{(17 ~-~ 8)^3}/{6}} +$
$+ {{4}/{24}} * [(17 ~-~ 11)^4 ~-~ (17 ~-~ 15)^4]= 0$ кН·м ³.

За найденными ординатами строим эпюры EI_y phi и EI_y w (рис. 2).

5) Графоаналитический метод.

Графоаналитическим способом определяем угол поворота и прогиб сечения при x = 4 м. Чертим фиктивную балку (рис. 4), загружаем распределенной фиктивной нагрузкой (эпюрой изгибающих моментов), которое заменяется фиктивными равнодействующими:

${P_1}$ ^ф ~ = 4 * 16 = 64 кН·м ²; ${P_2}$ ^ф ~ = {1/2} * 4 * 16 = 32 кН·м ²;

${P_3}$ ^ф ~ = {1/2} * 4 * 24 = 48 кН·м ²; ${P_4}$ ^ф ~ = 24 * 3 = 72 кН·м ²;

${P_5}$ ^ф ~ = {1/2} * 3 * (37,33 ~-~ 24) = 20 кН·м ²; ${P_6}$ ^ф ~ = {1/2} * 4 * (37,33 ~-~ 23,12) = 28,42 кН·м ²;

${P_7}$ ^ф ~ = 23,12 * 4 = 92,44 кН·м ²; ${P_8}$ ^ф $~ = {ql^3}/{12} = {4 * 4^3}/{12} = 21,33$ кН·м ²;

${P_9}$ ^ф ~ = {1/2} * 2 * 23,12 = 23,12 кН·м ².

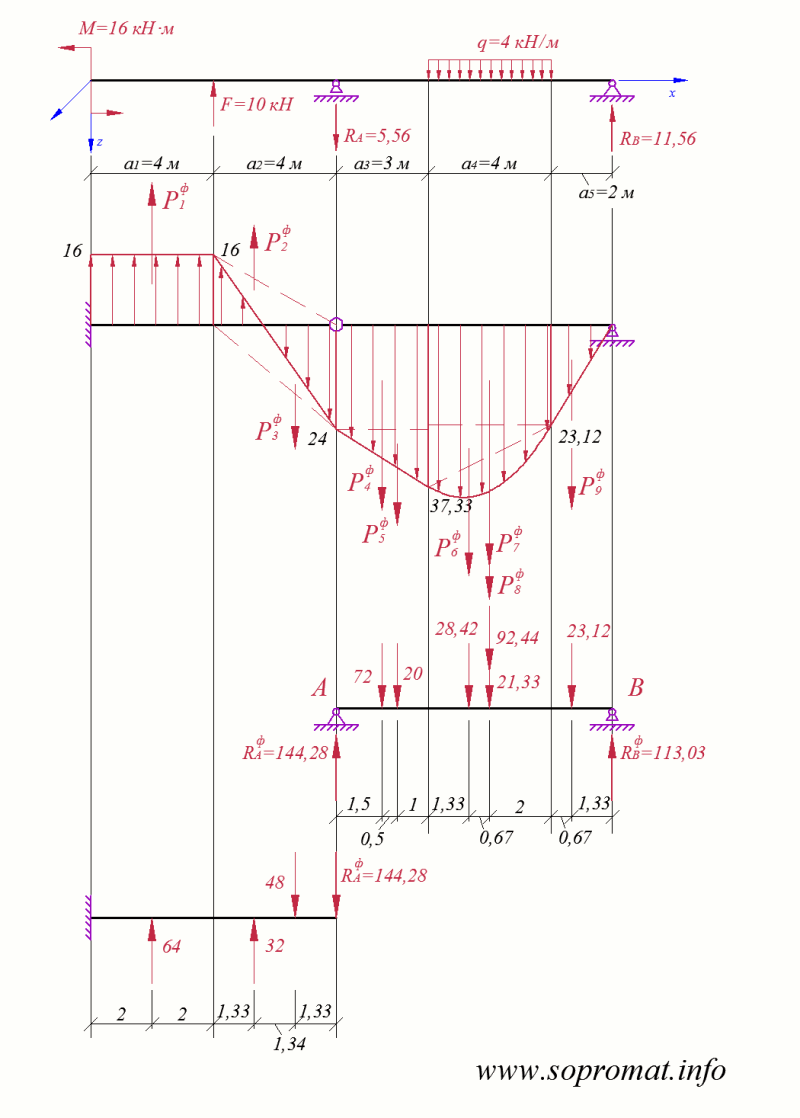
графо-аналитический метод определения перемещений при изгибе

Рис. 4

Вычисляем фиктивные опорные реакции:

$sum{~}{~}{M_A} = 0,~~ ~-~ R_B$ ^ф *9 + 72*1,5 + 20*2 + 28,42*4,33 + (92,44 + 21,33)*5 + 23,12*7,67 = 0,
~~ R_B ^ф ~= 113,03 кН·м ²;

$sum{~}{~}{M_B} = 0,~~ R_A$ ^ф *9 ~-~ 72*7,5 ~-~ 20*7 ~-~ 28,42*4,67 ~-~ (92,44 + 21,33)*4 ~-~
~-~ 23,12*1,33 = 0,
~~ R_A ^ф ~= 144,28 кН·м ².

Выполняем проверку: $sum{~}{~}{F_z} = 0,~~ ~-~ 144,28 + 72 + 20 + 28,42 + 92,44 + 21,33 + 23,12 ~-~ 113,03 = 0$ .

Определяем значение EI_y phi и EI_y w при x = 4 м:

EI_y phi = 144,28 + 48 ~-~ 32 = 160,28 кН·м ² рад;

EI_y w = ~-~ 144,28 * 4 ~-~ 48 * 2,67 + 32 * 1,33 = ~-~ 662,72 кН·м ³.

6) Метод Мора.

Для определения угла поворота и прогиба в сечении при x = 4 м методом Мора рассматриваем три состояния балки: грузовой и два единичных (рис. 5).

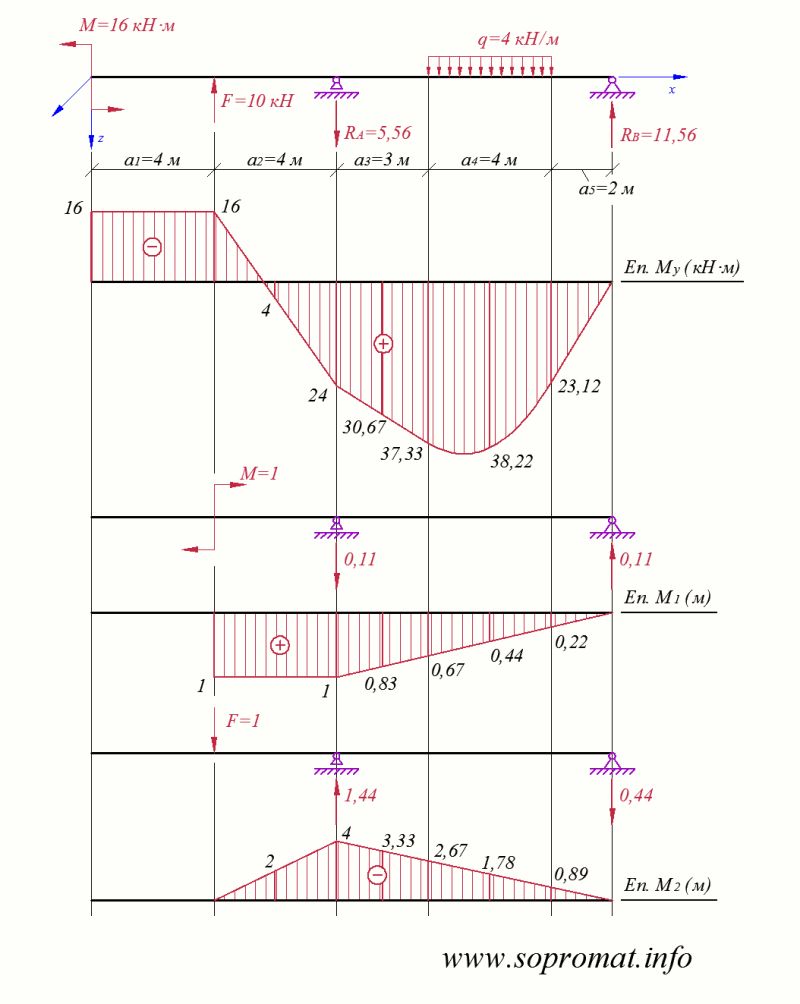
метод мора определения перемещений при изгибе

Рис. 5

Перемножая эпюры M_1 и M_2 на эпюру M_y (с использованием правила Верещагина и формулы Симпсона-Корноухова) получаем:

$EI_y phi = int{0}{l}{M_1 M_y dx} = 4 * 4 * 1 + {3/6} * (24 * 1 + 4 * 30,67 * 0,83 + 37,33 * 0,66) +$ + {4/6} * (37,33 * 0,66 + 4 * 38,22 * 0,44 + 23,12 * 0,22) + {1/2} * 2 * 23,12 * {2/3} * 0,22 = 159,72 кН·м ² рад;

$EI_y w = int{0}{l}{M_2 M_y dx} = ~-~ {4/6} * (4 * 4 * 2 + 24 * 4) ~-~ {3/6} * (24 * 4 + 4 * 30,67 * 3,33 + 37,33 * 2,67) ~-~$ ~-~ {4/6} * (37,33 * 2,67 + 4 * 38,22 * 1,78 + 23,12 * 0,89) ~-~ {1/2} * 2 * 23,12 * {2/3} * 0,89 = ~-~ 662,73 кН·м ³.